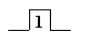С помощью чего в вычислительные устройства могут быть реализованы различные логические функции
Логические элементы компьютера
Вы будете перенаправлены на Автор24
Основные логические элементы реализуют 3 основные логические операции:
Связь между алгеброй логики и компьютерной техникой также лежит в двоичной системе счисления, которая используется в ЭВМ. Поэтому в устройствах ПК можно хранить и обрабатывать как числа, так и значения логических переменных.
Логический элемент компьютера – это часть электронной схемы, которая выполняет элементарную логическую функцию.
Переключательные схемы
В ЭВМ используются электрические схемы, которые состоят из большого количества переключателей. Переключатель, находясь в замкнутом состоянии ток пропускает, в разомкнутом – не пропускает. Работа таких схем удобно описывается при помощи алгебры логики. В зависимости от состояния переключателя можно регулировать получение или неполучение сигналов на выходах.
Вентили
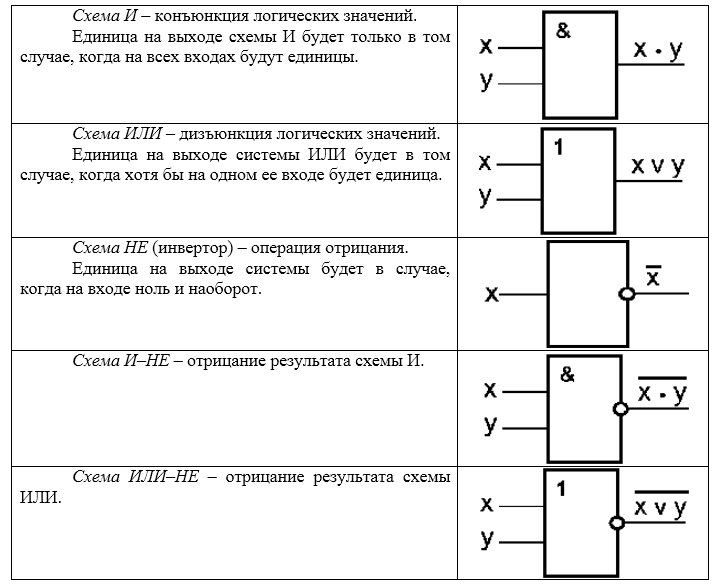
Среди логических элементов компьютеров выделяют электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (их называют вентили).
У каждого логического элемента есть условное обозначение, выражающее его логическую функцию, но не указывающее на электронную схему, которая в нем реализована. Такой подход реализован для упрощения записи и понимания сложных логических схем.
Готовые работы на аналогичную тему
Работа логических элементов описывается таблицами истинности.
Триггер
Триггеры и сумматоры состоят из вентилей.
Триггер – важнейшая структурная единица оперативной памяти ПК и внутренних регистров процессора.
Рисунок 3. Кратковременный импульс
Сумматор
Сумматоры широко применяются в арифметико-логических устройствах процессора и отвечают за суммирование двоичных разрядов.
Сумматор – логическая схема, которая способна суммировать 2 одноразрядных двоичных числа с переносом из предыдущего разряда.
Сумматор может находить применение и в других устройствах машины.
Для суммирования двоичных слов длиной от двух бит можно использовать последовательное соединение многоразрядных сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
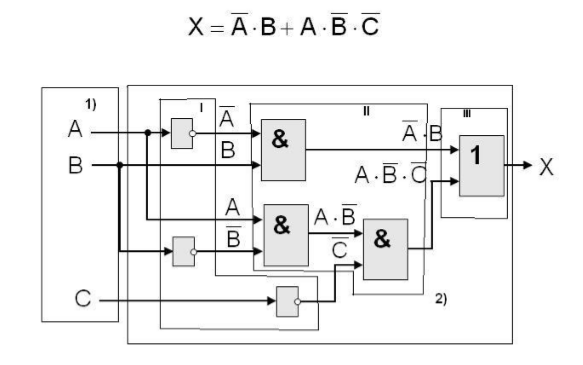
Пример реализации логической схемы
Алгоритм реализации:
С помощью базовых логических элементов реализуются основные операции в порядке их следования:
II – логическое умножение реализуется логическим элементом «И»;
III – логическое сложение реализуется логическим элементом «ИЛИ».
На выходе каждого элемента прописывается логическое выражение, которое реализуется данным элементом, что позволяет осуществить обратную задачу, т.е. по готовой схеме составить логическое выражение, которое реализует данная схема.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 12 04 2016
Тест по дисциплине вычислительная техника. Темы «Логические элементы. Триггер. Регистр.»


а) Устройство, выполняющее одну из логических операций
б) Устройство, необходимое для выполнения условия истинности или ложности
в) Устройство, необходимое для обработки сигналов и преобразования их в графическую информацию
г) Устройство, перерабатывающее информацию из одного вида в другой
а) Устройство, предназначенное для записи хранения цифровой информации
б) Устройство, для изменения токов в цепи
в) Устройство, необходимое для включения и выключения вычислительной техники
г) Устройство, регулирующее мощность
3)Что такое Регистр?
а) Совокупность триггеров
б) Устройство для визуального контроля
в) Манипулятор для ПК
г) Устройство, позволяющее осуществлять контроль операций
4)Чем оперирует Триггер?
а) Значениями двоичного кода
б) Короткими сигналами, поступающих хаотично
в) Логическими уравнениями
5) Чем оперирует Регистр?
а) Триггерами и значениями в них
6)Назовите виды регистров
а) Последовательные и непоследовательные
б) Параллельные и сдвига
в) Последовательные и регистр сдвига
г) Последовательные, параллельные и последовательно-параллельные
7)Какими способами может осуществляться ввод и вывод информации, рассматриваемой в регистре?
а) Однофазным и многофазным
б) Парафазным и однофазным
в) Парафазным и многофазным
г) Многофазным и не многофазным
8)Какое количество информации может хранить триггер?
г) до одного терабайта
9)Для чего используется регистры?
б) Для преобразования сигналов в слова
в) Для передачи информации
г) Для частичного преобразования токов
в) Не определено и является случайной величиной
г) Зависит от потенциалов токов и применяемой логики
Тема «Основные логические элементы. Триггеры. Регистры»
1)Что такое триггер?
Б) Устройство для запоминания цифровой информации
В Устройство для просмотра информации
Г) Это элемент информации
А) Схема статического триггера
3) Что такое регистр?(Два варианта ответов)
А) Упорядоченная последовательность триггеров
Б) Устройство для регистрации данных
В) Метод обработки информации
Г) Число триггеров соответствует числу разрядов в слове
4)Условное обозначение какого устройства представлено на рисунке?
Б)Условное обозначение параллельного 4-разрядного регистра
В) 4-разрядный триггер
Г) Триггер и регистор
5)Триггер 2 устойчивых состояния
6)Назовите недостающий вид регистров: параллельный, последовательный…
Г) Параллельный с триггером
Что называется логическим элементом?
А) Устройство, выполняющее одну из логических операций
Б) Устройство, необходимое для выполнения условия истинности или ложности
В) Устройство, необходимое для обработки сигналов и преобразования их в графическую информацию
Г) Устройство, перерабатывающее информацию из одного вида в другой
8)Регистр, в котором осуществляется сдвиг числа называется
А) Сдвинутым регистром
Б) Устройством ввода тока
В) Сдвигающим (регистр сдвига)
9) Как называют логический элемент «И»?
10)Использовать результат предыдущей опирации, выполеной комбинации называется
А) Элемент задержки
Г) Операция задержки
Тема «Основные логические элементы. Триггеры. Регистры»
1. Что используют для уплотнения каналов связи?
2. Как называется устройство, реализующее одну из логических операций?
а) Логический элемент
3. Как называют логический элемент «И»?
4. Назовите устройство, которое способно запоминать цифровую информацию?
5. Каким кодом осуществляется выбор входа по его номеру мультиплексор?
6. Вычислительная машина, которая обрабатывает информацию, представленную в аналоговой форме:
а) Аналоговая вычислительная машина (АВМ)
7. Что не относится к основным элементам пневматических АВМ?
в) Пневматические емкости.
8. С помощью чего в вычислительные устройства могут быть реализованы различные логические функции?
9. Элементарные логические элементы:
10. Устоичивое состояние триггера:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Ищем педагогов в команду «Инфоурок»
Вычислительная техника – самая динамичная и быстро развивающаяся область техники, которая затронула практически все виды человеческой деятельности.
Понятие «вычислительная техника» имеет два значения.
Во-первых, это область техники, объединяющая средства автоматизации математических вычислений обработки информации в различных сферах человеческой деятельности. Во-вторых, это наука о принципах построения, действия и проектирования этих средств.
В курсе дисциплины «Вычислительная техника» студенты рассматривают типовые элементы вычислительной техники.
Тест предназначен для контроля знаний по разделу «Типовые элементы вычислительной техники»
Студент должен знать:
— назначение типовых элементов;
— основные логические элементы
— характеризовать и классифицировать основные логические элементы.
Номер материала: 133975
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Итоговое сочинение успешно написали более 97% выпускников школ
Время чтения: 2 минуты
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Российские юниоры завоевали 6 медалей на Международной научной олимпиаде
Время чтения: 2 минуты
Чем заняться с детьми в новогодние праздники в Москве
Время чтения: 4 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Лекция 3. Логические основы работы ЭВМ
3.1. Что такое алгебра логики
| Алгебра логики — это раздел математики, изучающий логические переменные, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. |
3.2. Какая связь между алгеброй логики и двоичным кодированием
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
3.3. В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
3.4. Что такое логический элемент компьютера
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями ), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
3.5. Что такое схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 3.1.
Таблица истинности схемы И
| x | y | x & y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x & y (читается как «x и y» ). Операция конъюнкции на структурных схемах обозначается знаком «&» (читается как «амперсэнд» ), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 3.2. Знак «1» на схеме — от устаревшего обозначения дизъюнкции как «>=1» (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как «x или y» ).
Таблица истинности схемы ИЛИ
| x | y | x v y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
С х е м а НЕ
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке 3.3.
Таблица истинности схемы НЕ
| x | |
| 0 | 1 |
| 1 | 0 |
С х е м а И—НЕ
Таблица истинности схемы И—НЕ
| x | y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
С х е м а ИЛИ—НЕ
Таблица истинности схемы ИЛИ—НЕ
| x | y | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
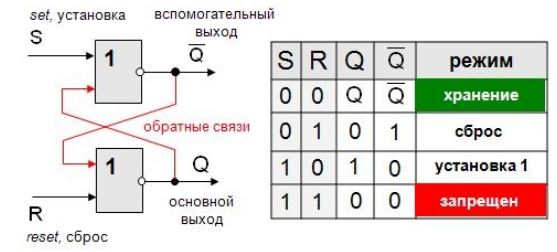
3.6. Что такое триггер
| Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. |
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рис. 3.6.
На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( ).
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.
На рис. 3.7 показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.
| S | R | Q | |
| 0 | 0 | запрещено | |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | хранение бита | |
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 2 10 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
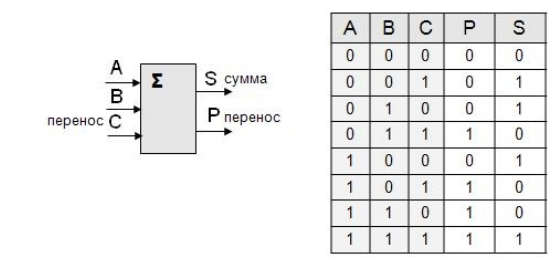
3.7. Что такое сумматор
| Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. |
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
1. цифра a i первого слагаемого;
2. цифра b i второго слагаемого;
3. перенос p i–1 из младшего разряда.
В результате сложения получаются две цифры:
1. цифра c i для суммы;
2. перенос p i из данного разряда в старший.
| Входы | Выходы | |||
| Первое слагаемое | Второе слагаемое | Перенос | Сумма | Перенос |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Например, схема вычисления суммы C = (с 3 c 2 c 1 c 0 ) двух двоичных трехразрядных чисел A = (a 2 a 1 a 0 ) и B = (b 2 b 1 b 0 ) может иметь вид:
3.8. Какие основные законы выполняются в алгебре логики
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений :
ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
| Закон | Для ИЛИ | Для И |
| Переместительный | ||
| Сочетательный | ||
| Распределительный | ||
| Правила де Моргана | ||
| Идемпотенции | ||
| Поглощения | ||
| Склеивания | ||
| Операция переменной с ее инверсией | ||
| Операция с константами | ||
| Двойного отрицания |
3.9. Как составить таблицу истинности
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
| Переменные | Промежуточные логические формулы | Формула | |||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
2. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
3. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
3.10. Как упростить логическую формулу
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1)
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2)
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
4)
( вводится вспомогательный логический сомножитель ( ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
5)
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6)
(выносятся за скобки общие множители; применяется правило операций с константами);
7)
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8)
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);
9)
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10)
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
3.11. Что такое переключательная схема
В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
| Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. |
Найдем функции проводимости F некоторых переключательных схем:
Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.
Задача нахождения среди равносильных схем наиболее простых является очень важной. Большой вклад в ее решение внесли российские учёные Ю.И. Журавлев, С.В. Яблонский и др.
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
1. Построим схему, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трёх контактов.
2. Построим схему с пятью переключателями, которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из этих переключателей.
3. Найдем функцию проводимости схемы:
4. Упростим переключательные схемы: