Три точки лежат на одной прямой докажи что можно построить плоскость

Через три точки можно провести плоскость

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Существование плоскости, проходящей через три данные точки

Существование плоскости, проходящей через три данные точки

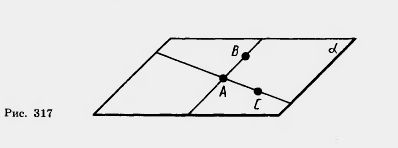
Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Доказательство. Пусть А, В, С — три данные точки, не лежащие на одной прямой (рис. 317). Проведем прямые АВ и АС; они различны, так как точки А, В, С не лежат на одной прямой. По аксиоме Сз через прямые АВ и АС можно провести плоскость . Эта плоскость содержит точки А, В, С.

Докажем, что плоскость а, проходящая через точки А, В, С, единственна. Действительно, плоскость, проходящая через точки А, В, С, по теореме 15.2 содержит прямые АВ и АС. А по аксиоме Сз такая плоскость единственна.

Задача (13). Можно ли провести плоскость через три точки, если они лежат на одной прямой? Объясните ответ.

Решение. Пусть А, В, С — три точки, лежащие на прямой . Возьмем точку D, не лежащую на прямой (аксиома I). Через точки А, В, D можно провести плоскость (теорема 15.3). Эта плоскость содержит две точки прямой — точки A и В, а значит, содержит и точку С этой прямой (теорема 15.2).

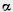
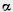
Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

сколько плоскостей можно провести через

две различные точки

три различные точки

четыре точки никакие три из которых не лежат на одной прямой.

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

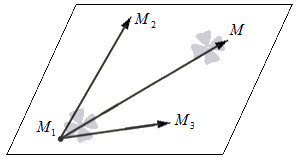
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

На схеме это будет выглядеть так:

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Решение

Используем поочередно оба способа.

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Решение

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

Источник

Когда 3 точки лежат на одной прямой

Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.

Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.

Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.

Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.

Решим поставленную задачу

Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:

После преобразования получим:

Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.

Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)

Источник

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

На схеме это будет выглядеть так:

Запишем полученное уравнение в координатной форме:

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Решение

Используем поочередно оба способа.

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

Мы получили нужное нам уравнение.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Решение

Векторное произведение будет равно:

Если мы используем второй способ, у нас получится:

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

Источник

Введение (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

Никакие два из них не будут линейно зависимые. Покажем, что векторы + , и + + линейно независимы. Предположим противное, то есть. эти векторы линейно зависимы, а следовательно, выполняется векторное равенство: a( + ) + b( + + ) = , a2 + b2 ¹ 0. Перепишем это равенство в виде:

(a + b) + (a + b) + b =

Так как векторы базиса , , – линейно независимы, то выше приведенное равенство выполняется, только при a и b равных нулю одновременно. Получили противоречие с предположением. Значит, векторы + , и + + линейно независимы.

Аналогично можно доказать линейную независимость остальных пар векторов.

Векторы этой системы порождают точки:

E1 = π(), E2 = π(), E3 = π(), E4 = π( + ), E5 = π( + ), E6 = π( + ), E7 = π( + + )

Точки E1 – E7, порождённые неколлинеарными векторами, различны.

Доказать, что на проективной плоскости P(V) существуют четыре точки, из которых никакие три не лежат на одной прямой.

Так как dim(P(V)) = 2, то векторное пространство, порождающее проективную плоскость P(V) имеет размерность 3. B = <, , > – базис векторного пространства V. Векторы базиса , , линейно независимы, значит точки E1, E2, E3, порождённые этими векторами, не лежат на одной прямой. Рассмотрим E1 = π(), E2 = π(), E3 = π(), E = π( + + ).

Возьмем точки E1, E2, E и покажем, что они не лежат на одной прямой.

Нам достаточно показать, что векторы , , , порождающие эти точки линейно независимые.

Предположим, что , , – линейно зависимые. По определению линейной зависимости имеем:

l1 + l2 + l3 =

+ + ¹ 0

l1 + l2 + l3( + + ) =

(l1 + l3) + (l2 + l3) + l3 =

Так как векторы , , по условию являются линейно независимыми, то это векторное равенство выполняется только при l1, l2, l3 равных нулю одновременно. Наше предположение не верно. Значит векторы , , линейно независимые, а точки E1, E2, E не лежат на одной прямой.

Аналогично доказывается, что тройки точек E1, E3, E и E2, E3, E не лежат на одной прямой.

Задачи для самостоятельного решения.

1. – трёхмерное векторное пространство над полем F3 вычетов по модулю 3. Сколько точек содержит произвольная прямая проективной плоскости P()?

2. Сколько прямых содержит плоскость P()?

3. Доказать, что проективная прямая содержит по крайней мере три точки.

4. Доказать, что на проективной плоскости существуют три точки, не лежащие на одной прямой.

5. Доказать, что любые две прямые проективной плоскости пересекаются.

6. Доказать, что через две различные точки проективной плоскости можно провести прямую.

7. Каково наименьшее число точек проективного пространства P3(K) над полем K.

8. Доказать, что в n-мерном проективном пространстве (n + 2) точки общего положения.

9. Сколько точек содержит произвольная прямая n-мерного проективного пространства P()?

10. – (n + 1)- мерное векторное пространство над полем Fp вычетов по модулю p, где p – простое число. Доказать, что n-мерное проективное пространство P() состоит из точек.

§ 3. Проективные координаты на проективной прямой и проективной плоскости

1. Определение. Проективным репером на проективной прямой называют упорядоченную совокупность трех различных точек A1, A2, E прямой.

Точки A1, A2, называют координатными точками, а E – единичной точкой репера.

Возьмем любую точку M проективной прямой P1. Возьмем в векторном пространстве V2, порождающем проективную прямую P1, базис, согласованный с репером R B = <, >, то есть π() = A1, π() = A2, π( + ) = E. Пусть Î V2, ¹ . π() = М, разложим его по базисным векторам: = х1 + х2, = (х1, х2)R.

Проективными координатами точки на проективной прямой относительно проективного репера R будем называть координаты вектора, порождающего данную точку относительно базиса векторного пространства, согласованного с репером R.

Обозначим М = (х1, х2)R. Возьмем = l, l ¹ 0, также порождает точку М: π() = М, = lх1 + lх2.

Из определения проективных координат точки заключаем, что точка М имеет координаты (lх1, lх2) относительно репера R.

Таким образом, проективные координаты точки на проективной прямой определяются с точностью до постоянного множителя.

На расширенной прямой задан проективный репер R = <A1, A2, E> построить точку M(2, 3) по её координатам в этом репере.

Пусть V2 – векторное пространство порождающее прямую : p(V2\<>) = .

В роли V2 возьмём множество направленных отрезков с началом в точке O Î . Обозначим B = <, > базис векторного пространства V2, согласованный с репером R или векторный базис проективного репера [2]. Решение задачи проводим по следующей схеме:

1. Восстановим векторный базис проективного репера R = <A1, A2, E>. Для этого возьмём любой вектор , порождающий точку E и строим векторы и , сумма которых даёт вектор . B = <, > – векторный базис проективного репера. Векторы и порождают соответственно точки A1 и A2 (см. рис. 17).

2. Строим вектор = 2 + 3.

3. Строим точку M, порожденную вектором , как пересечение прямой и m, для которой вектор служит направляющим.

На расширенной прямой задан проективный репер R = <A1, A2, Eµ>. Построить точку M(–1, 2) относительно репера R.

1. Найдём векторный базис проективного репера R = <A1, A2, Eµ>. Так как. Eµ – несобственная точка прямой , то вектор, её порождающий, является направляющим вектором прямой d0, параллельной прямой d. Возьмем точку O Î d0, и векторный базис B = <, >, репер R: π() = A1, π() = A2, π() = Eµ. (см. рис. 18).

2. Строим вектор = – + 2.

3. М = m Ç .

2. Перейдем теперь к определению проективных координат на проективной плоскости.

2 Определение. Проективным репером на проективной плоскости называется упорядоченная совокупность четырех точек общего положения R = <A1, A2, A3, E>.

Базис В = <, , > векторного пространства, порождающего проективную плоскость, будем называть согласованным с репером R, если векторы , , порождают соответственно точки A1, A2, A3, а их сумма порождает точку Е, Рис 19. В символической записи это выглядит так:

π() = A1, π() = A2, π() = A3, + + = , π() = E.

Возьмем произвольную точку М проективной плоскости P2. Пусть – вектор, порождающий точку М, то есть π() = М. Система векторов , , , линейно зависима.

Тогда = x1 + x2 + x3.

Определение. Проективными координатами точки М на проективной плоскости относительно проективного репера R называют координаты вектора, порождающего данную точку относительно базиса векторного пространства, согласованного с репером R.

То есть точка М имеет координаты (x1, x2, x3) относительно проективного репера R. Так как вектор = l, l ¹ 0 порождает ту же точку М, а <lx1, lx2, lx3>,то точка М относительно репера R будет иметь также координаты (lx1, lx2, lx3).

Таким образом, проективные координаты точки определяются с точностью до постоянного множителя.

Как построить точку по ее координатам?

Пусть на проективной плоскости задан R = <A1, A2, A3, E>.

Совокупность трех точек A1, A2, A3 проективной плоскости и трех прямых (A1A2), (A1A3), (A2A3) называют координатным трехвершинником (треугольником).

Пусть точка М задана координатами x1, x2, x3.

Рассмотрим отображение множества P2 \ A3 на координатную прямую A1A2, то есть проектируем это множество на прямую A1A2 с центром A3.

Точке М Î P2 \ A3 ставим в соответствие точку M3 = (A3M) Ç (A1A2), E3 = (A3E) Ç (A1A2). На прямой (A1A2) рассмотрим проективный репер R3 = <A1, A2, E3>. Оказывается, что M3 будет иметь координаты (x1, x2) относительно проективного репера R3.

Спроектируем теперь множество P2 \ A1 на прямую A2A3.Точке М Î P2 \ A1 поставим в соответствие точку M1 = (A1M) Ç (A2A3). На проективной прямой A2A3 возникает проективный репер R1 = <A2, A3, E1>, E1 = (A1E) Ç (A2A3). Точка М1 относительно репера R1 на прямой A2A3 будет иметь координаты (x2, x3). Аналогично, точка М2 будет иметь координаты (x1, x3) в репере R2 = <A1, A3, E2> на прямой A1A3. Тогда M = (A1M1) Ç (A2M2) Ç(A3M3).

На расширенной плоскости задан проективный репер R = <A1, A2, A3, E>. Построить точку M(1, 1, 2) относительно репера R.

Решение.

Обозначим через E3 проекцию единичной точки репера R из центра A3 на прямую A1A2. Упорядоченная тройка точек A1, A2, Е3 образует на прямой A1A2 проективный репер R3 = <A1, A2, E3>. Относительно репера R3 проекция M3 точки M из центра A3 на прямую A1A2 имеет координаты (1, 1), то есть точка M3 совпадает с точкой E3. Аналогично можно ввести реперы R2 = <A1, A3, E>, R1 = <A2, A3, E> и построить ещё одну проекцию точки М. Построим, например, точку M2 относительно репера R2 (построение в задаче 1).

Тогда точка M находится как пересечение прямых A3M3 и A2M2 (см. рис. 20).

На расширенной плоскости задан проективный репер R = <A1, A2, A3, Eµ>, где точки A1, A2, A3 – собственные, а точка Eµ – несобственная. Построить точку М(1, 1, 2) по её координатам в репере R.

Считаем, что точка Eµ является несобственной точкой прямой . Строим точку E1, которая является проекцией точки Eµ на прямую A2A3 из точки A1. (Для этого на через точку A1 проводим прямую паралельную прямой , которая в пересечении с прямой A2A3 даст точку E1). E1 = М1.

Тогда точку М несложно построить: М = (A1M1) Ç (A2M2) (см. рис. 21).

На расширенной плоскости задан проективный репер R = <Xµ, Yµ, A3, E>. Построить точку M(4, –1, 2) по её координатам в репере R.

Две вершины координатного треугольника несобственные: Xµ, Î , Yµ Î , d1 È Xµ = , d2 È Yµ = .

1. Строим проекции точки Е на прямые и : Е1 = (ЕХ¥) Ç , Е2 = (Е Yµ) Ç .

2. Строим проекции точки М:

1. М1(–1, 2) относительно проективного репера R1 = <Yµ, A3, E1> прямой ;

2. М2(4, 2) или М2(2, 1) относительно проективного репера R2 = <Xµ, A3, E> прямой .

Однородные и неоднородные координаты на расширенной прямой и расширенной плоскости

Возьмем на расширенной плоскости расширенную прямую и рассмотрим проективный репер R¥ = <A¥, А2, E>. Возьмем точку О, не принадлежащую прямой , и построим тройку векторов , , , Пусть произвольная точка М относительно проективного репера R¥ имеет координаты М(х1, х2). На прямой рассмотрим аффинный репер <А2, >, порожденный проективным репером R¥ = <A¥, А2, E>. Пусть х – координата точки М в аффинном репере , то есть

Следовательно, точка М имеет координаты (х, 1) относительно репера R¥.

Учитывая, введенные выше обозначения для проективных координат точки М, получим х = lх1, 1 = lх2.

Отсюда l = и .

Таким образом, аффинные координаты собственной точки М равны отношению проективных координат этой точки в репере R¥: .

Следовательно, мы установили связь между аффинными координатами и проективными координатами собственных точек прямой . (х1, х2) называют однородными координатами точки М. (х) называют неоднородными координатами точки М.

Рассмотрим неоднородные координаты на расширенной плоскости.

На расширенной аффинной плоскости возьмем проективный репер R¥ = <X¥, Y¥, А3, E>.

Источник