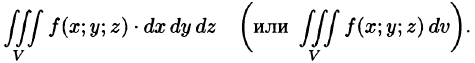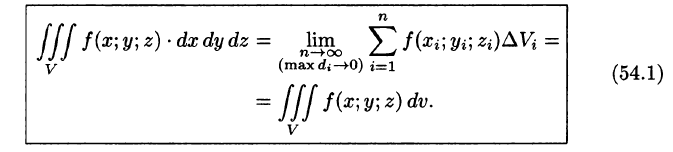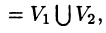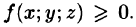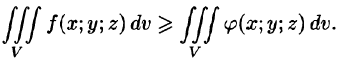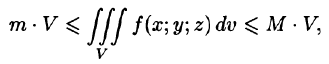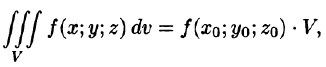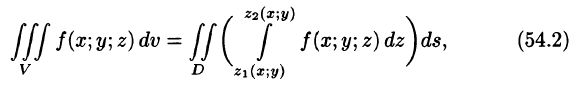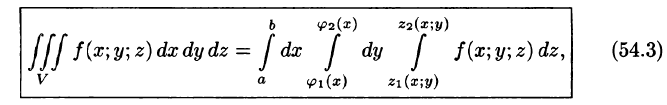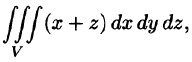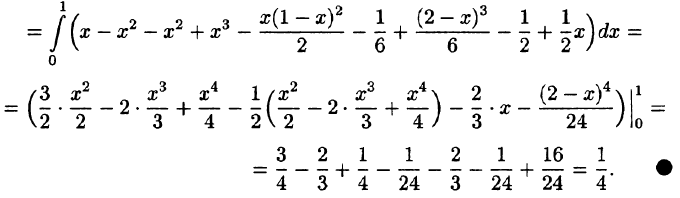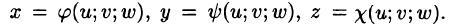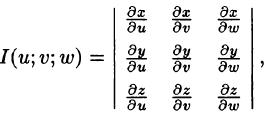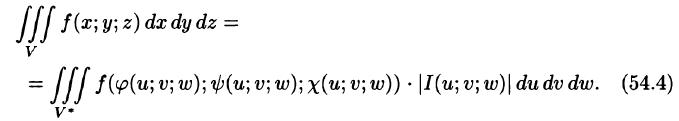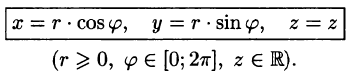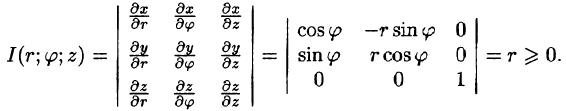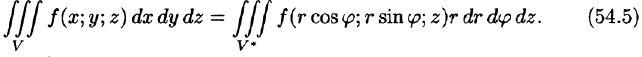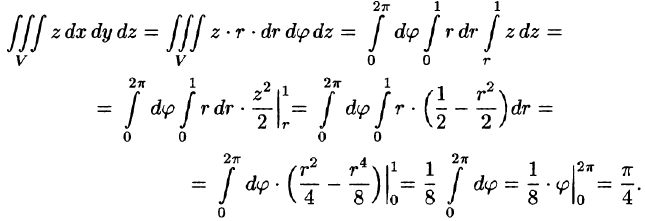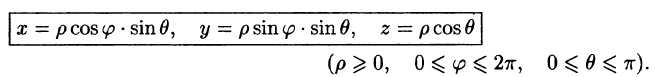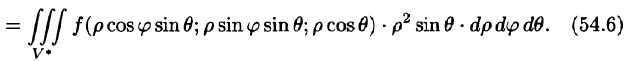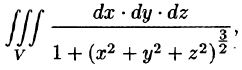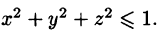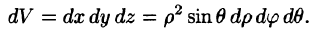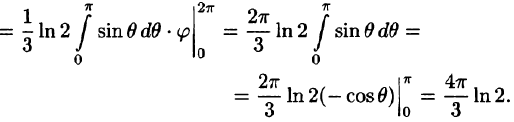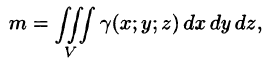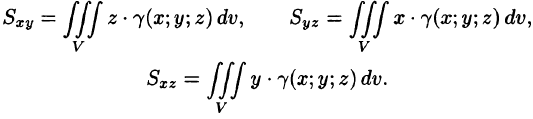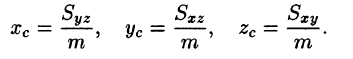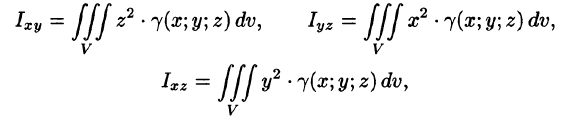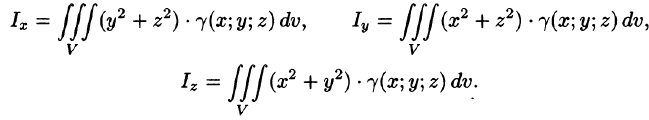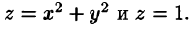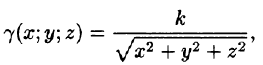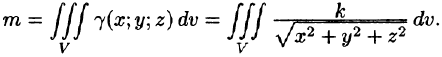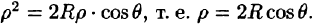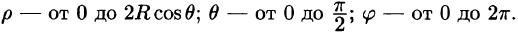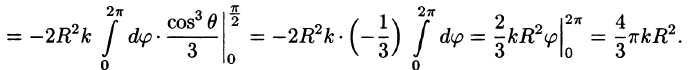Тройной интеграл это что
Лекции Тройной интеграл
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
Вычисление тройного интеграла в сферических координатах.
S =
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы 
Таким образом,


В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область V разбита на области V 1 и V2, то

4) Объем тела V равен

Вычисление тройного интеграла в декартовых координатах.
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:

В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
Решение. Вычислим объём при помощи тройного интеграла по формуле (2)
Перейдем к повторному интегралу по формуле (3).
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество

Тройной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей 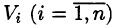
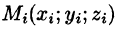
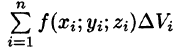
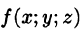
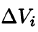
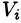
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» 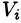
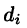
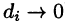
Таким образом, по определению, имеем:
Здесь dv = dx dy dz — элемент объема.
Теорема:
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при 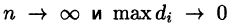
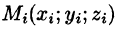
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
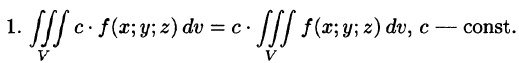
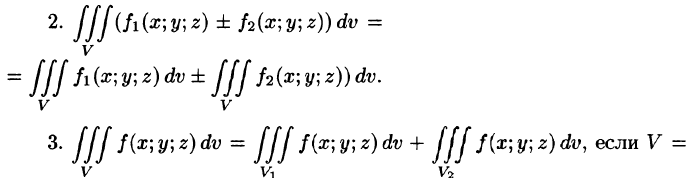
а пересечение 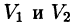
4. 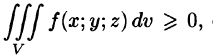
Если в области интегрирования 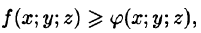
5.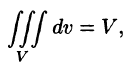
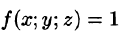
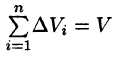
6. Оценка тройного интеграла:
где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.
7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 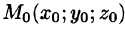
где V — объем тела.
Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
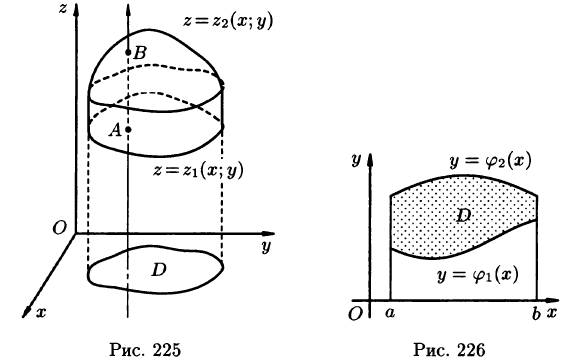
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью 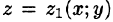
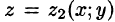
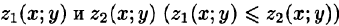
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. 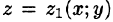
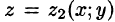
Если область D ограничена линиями 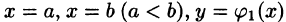
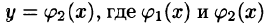
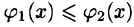
по которой вычисляется тройной интеграл в декартовых координатах.
Замечания:
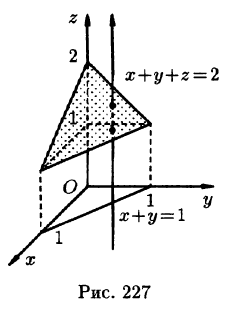
Пример:
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).
Решение:
Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:
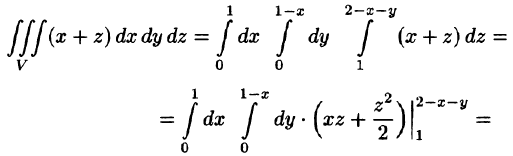
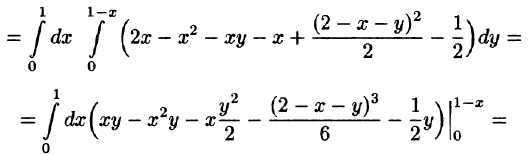
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка
Если эти функции имеют в некоторой области 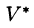
то справедлива формула замены переменных в тройном интеграле:
Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).
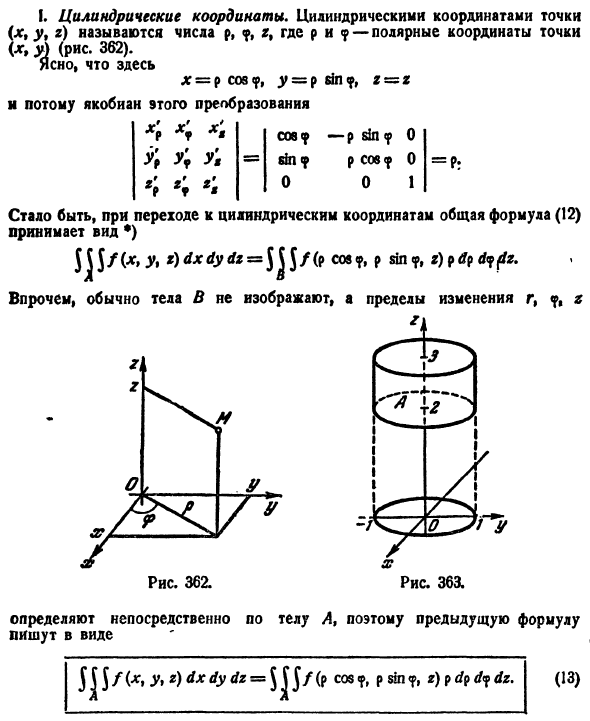
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
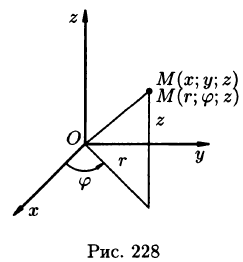
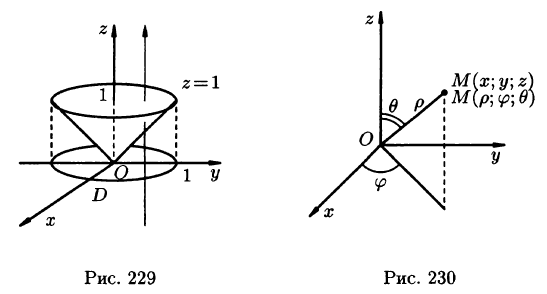
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел 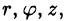
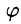
Эти три числа (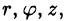
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
Возьмем в качестве и, v, w цилиндрические координаты 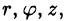
Формула замены переменных (54.4) принимает вид
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 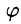
Замечание:
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
Пример:
Вычислить 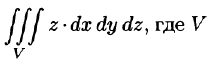
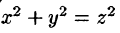
Решение:
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: 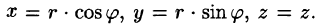
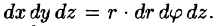
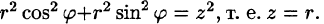
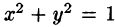
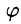
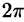
Таким образом, согласно формуле (54.5), получаем:
Заметим, что, не переходя к цилиндрическим координатам, получим:
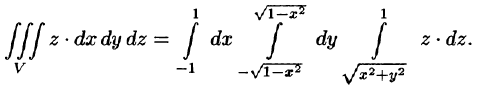
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел 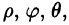
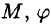
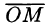
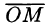
Сферические координаты 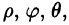
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
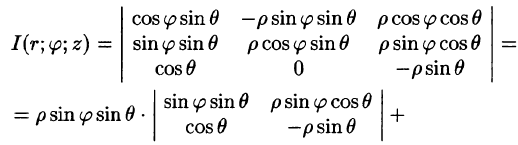
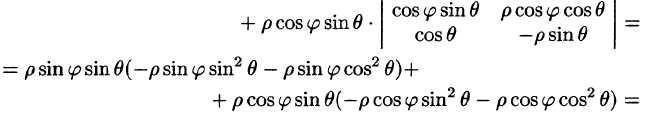
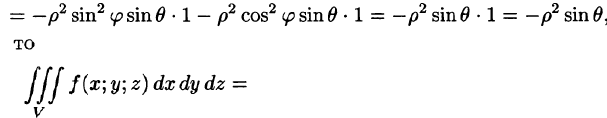
Замечание:
Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 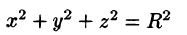
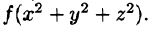
Пример 54.3. Вычислить
где V — шар
Решение:
Вычислим интеграл путем перехода к сферическим координатам: 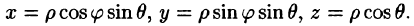
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид 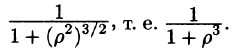
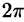
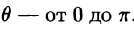
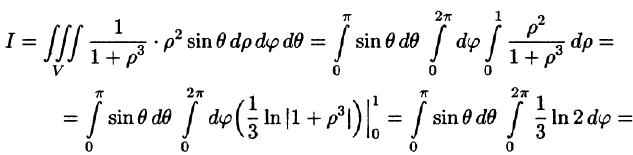
Некоторые приложения тройного интеграла Объем тела
Объем области V выражается формулой 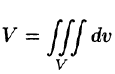
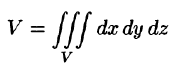
Масса тела
Масса тела m при заданной объемной плотности 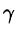
где 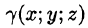
Статические моменты
Моменты 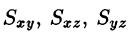
Центр тяжести тела
Координаты центра тяжести тела V находятся по формулам
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей:
Пример:
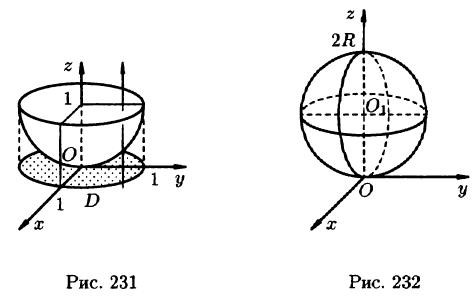
Найти объем тела, ограниченного поверхностями
Решение:
Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом 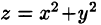
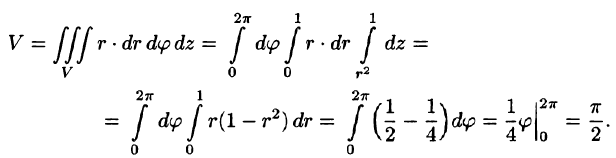
Пример:
Найти массу шара 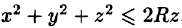
Решение:
Уравнение сферы 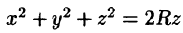
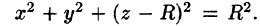
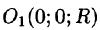
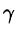
где k — коэффициент пропорциональности, 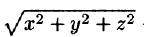
Итак,
Вычислять интеграл будем в сферических координатах. Уравнение сферы 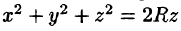
Поэтому сферические координаты будут изменяться в следующих пределах:
Подынтегральная функция примет вид 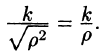
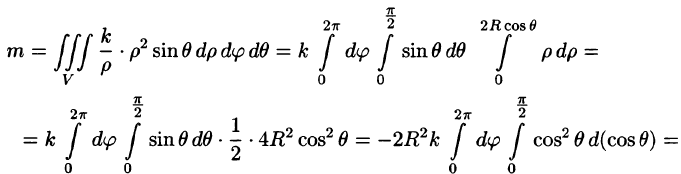
Из соображений симметрии следует, что 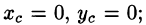
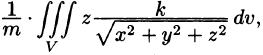
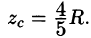
Тройной интеграл


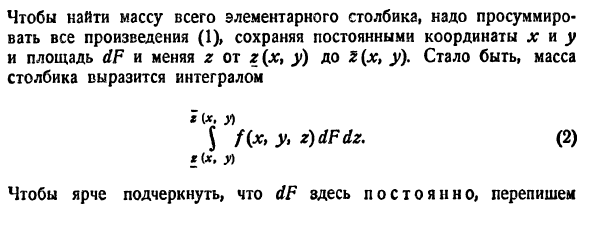

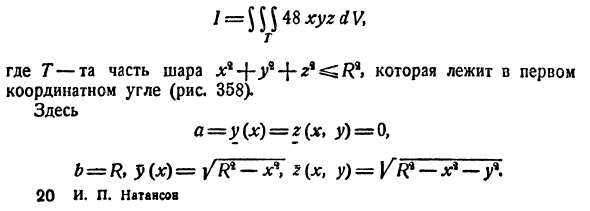

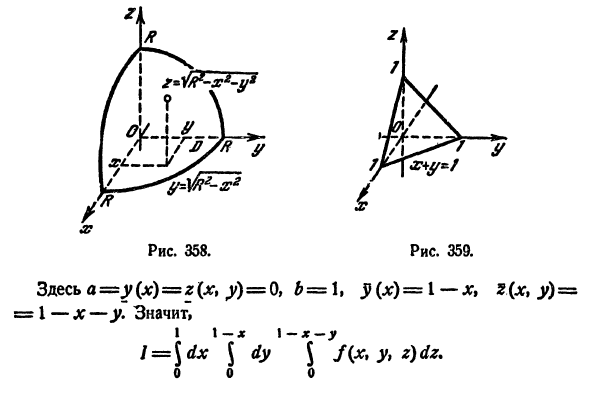

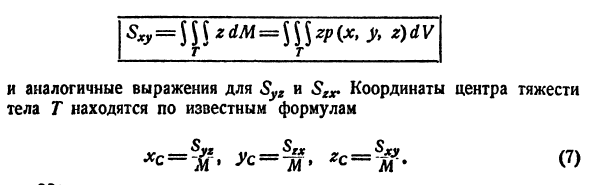









Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института