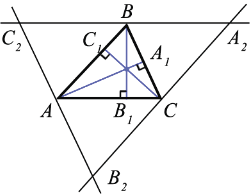
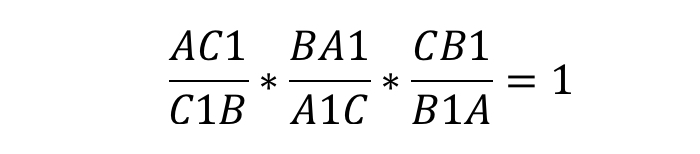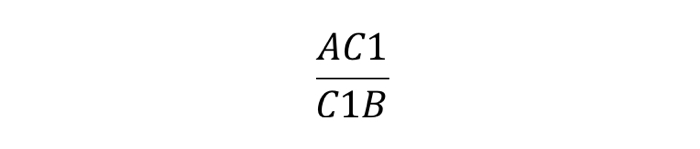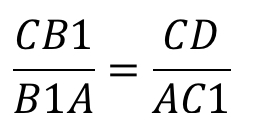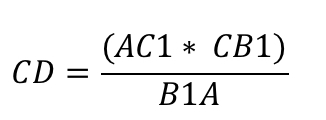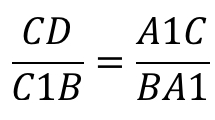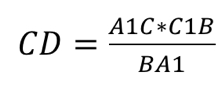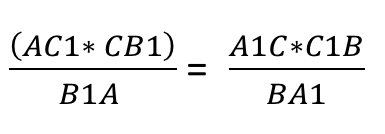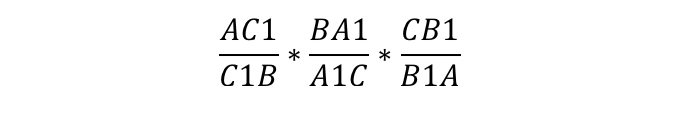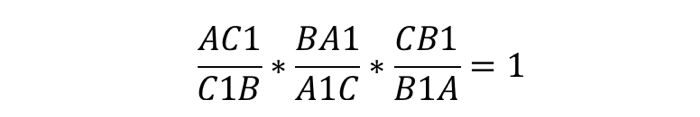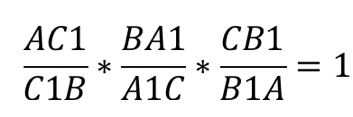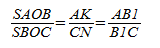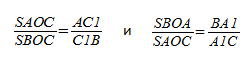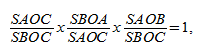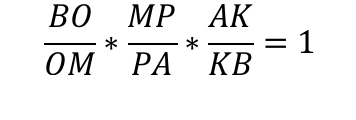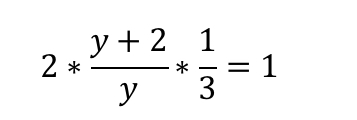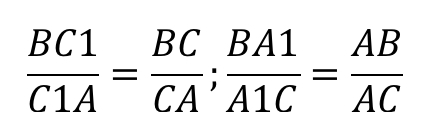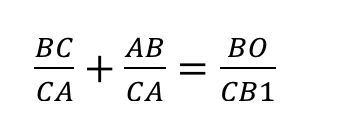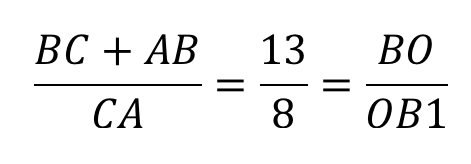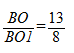С помощью теоремы чевы докажите что высоты треугольника пересекаются в одной точке

Теорема о пересечении высот треугольника

Теорема

Доказательство

Доказать: АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

Доказательство:

Проведём через каждую вершину АВС прямую, параллельную противоположной стороне.

Получим А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁А₂В₂, АА₁В₂С₂ и ВВ₁А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, они пересекаются в одной точке. Теорема доказана.

Замечательные точки треугольника : точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).

Поделись с друзьями в социальных сетях:

Источник

Теорема Чевы: формулировка и пример с решением

В данной публикации мы рассмотрим одну из классических теорем аффинной геометрии – теорему Чевы, которая получила такое название в честь итальянского инженера Джованни Чевы. Также разберем пример решения задачи, чтобы закрепить представленный материал.

Формулировка теоремы

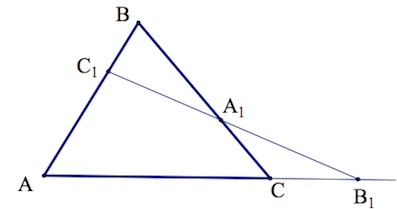
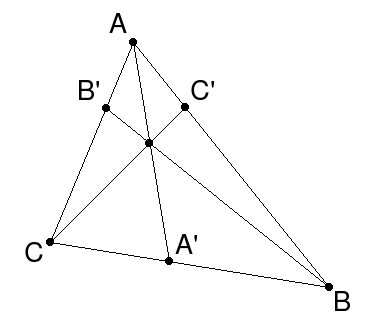
Дан треугольник ABC, в котором каждая вершина соединена с точкой на противоположной стороне.

Таким образом, мы получаем три отрезка (AA’, BB’ и CC’), которые называются чевианами.

Данные отрезки пересекаются в одной точке тогда и только тогда, когда выполняется следующее равенство:

Теорему можно, также, представить в таком виде (определяется, в каком соотношении точки делят стороны):

Тригонометрическая теорема Чевы

Примечание: все углы – ориентированные.

Пример задачи

Дан треугольник ABC с точками A’, B’ и C’ на сторонах BC, AC и AB, соответственно. Вершины треугольника соединены с данным точками, и образованные отрезки проходят через одну точку. При этом точки A’ и B’ взяты на серединах соответствующих противоположных сторон. Выясните, в каком соотношении точка C’ делит сторону AB.

Решение
Нарисуем чертеж согласно условиям задачи. Для нашего удобства примем следующие обозначения:

Остается только составить соотношение отрезков согласно теореме Чевы и подставить в него принятые обозначения:

После сокращения дробей получаем:

Значит, AC’ = C’B, т.е. точка C’ делит сторону AB пополам.

Следовательно, в нашем треугольнике отрезки AA’, BB’ и CC’ являются медианами. Решив задачу мы доказали, что они пересекаются в одной точке (справедливо для любого треугольника).

Примечание: с помощью теоремы Чевы можно доказать, что в треугольнике в одной точке, также, пересекаются биссектрисы или высоты.

Источник

Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.

Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.

Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.

Формулировка теоремы Менелая

Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.

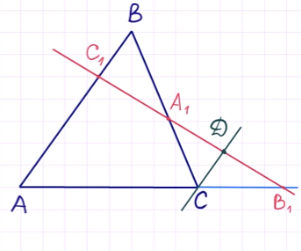
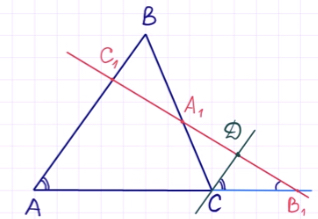
Прежде чем приступить к проработке, сделаем соответствующий рисунок.

Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.

Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.

Если мы видим приведённый выше рисунок, можно записать формулу:

Доказательство теоремы

Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:

Обозначим точку пересечения данной прямой с B₁C₁ через точку D.

В таком случае мы получим несколько пар подобных треугольников.

Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B₁CD и B₁AC₁. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B₁ между ними.

Углы B₁CD и B₁AC₁ равны как соответственные при параллельных прямых CD, AB и секущей AC.

Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:

Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.

Используя описанное равенства, применив свойства пропорции, запишем:

Запишем следующую пару подобных треугольников: треугольники CDA₁ и BC₁A₁ подобны, так как углы CA₁D и BA₁C₁ равны как вертикальные. Кроме этого, угол CDA₁ равен углу BC₁A₁, как накрест лежащие при параллельных прямых CD, AB и секущей C₁D.

Покажем это на рисунке:

Из данного подобия можно записать некоторую пропорциональность сходственных сторон:

Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.

Таким образом получаем:

Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:

Что и требовалось доказать.

Формулировка теоремы Чевы

Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.

Рассматриваемая теорема была доказана ученым в 1678 г.

Рассмотрим приведённый ниже рисунок:

Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:

В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».

Доказательство теоремы

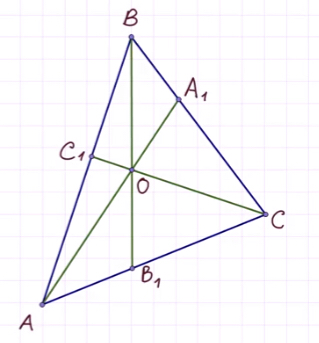
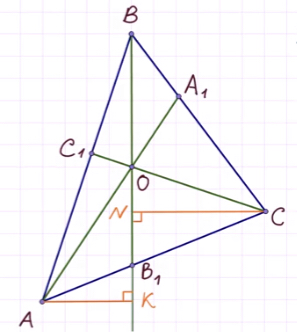
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.

Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:

Обозначим за O точку пересечения данных прямых.

Продлим медиану BB1.

Проведём перпендикуляры из вершин A и С таким образом:

Треугольники AKB₁ и CNB₁ подобны по острому углу.

Теперь перемножим равенства:

что и требовалось доказать.

Применение теорем Чевы и Менелая при решении задач ЕГЭ

Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.

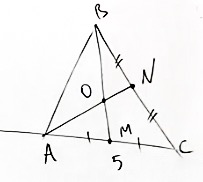
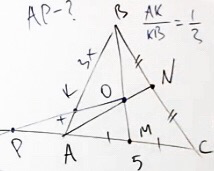
Задача 1

Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.

Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.

Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.

Сторону AP обозначим за y.

Найти: чему равен отрезок AP.

Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.

Рассмотрим треугольник ABM. Для него берём прямую OP.

Таким образом мы нашли искомые точки P, A, M, O, K и B.

Запишем теорему Менелая к данному рисунку.

Подставляем в это соотношение известные данные:

В итоге мы получаем, что y = 4.

Ответ: отрезок AP = 4 см.

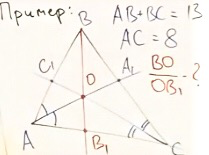
Задача 2

Задача, связанная со свойствами теоремы Чевы.

сумма AB и BC равна 13;

Найти: отношение BO и OB1.

Итак, запишем отношение:

Конечным результатом является дробь 13/8.

Источник

Обобщающий урок «Теоремы Менелая и Чевы»

Разделы: Математика

Оборудование: мультимедийный проектор. Приложение 1.

1. Организационный момент.

Точка С₁ делит сторону АВ треугольника АВС в отношении 2 : 1. точка В₁ лежит на продолжении стороны АС за точку С, и АС = СВ₁. В каком отношении делит прямая В₁ С₁ сторону ВС? (на слайде 2).

Решение: По условиюИспользуя теорему Менелая, находим: .

В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.

В каком отношении точка К делит АС, считая от точки А? (на слайде 3).

В треугольнике АВС на стороне ВС взята точка N так, что NС = 3ВN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая МN пересекает сторону АВ в точке F. Найдите отношение . (на слайде 4).

Решение: По условию задачи МА = АС, NС = 3 ВN. Пусть МА = АС = b, BN = k, NC = 3k. Прямая МN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

На стороне PQ треугольника PQR взята точка N, а на стороне РR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QR в отношении m : n, считая от точки Q. Найдите PN : PR. (на слайде 5).

Решение: По условию NQ = LR, . Пусть NA = LR = a, QF =km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая

3. Отработка практических навыков.

Докажите теорему: Медианы треугольника пересекаются в одной точке; точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины. (рисунок 1 слайд 6).

Доказательство: Пусть АМ₁, ВМ₂, СМ₃ – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по теореме Чевы (обратной) отрезки АМ₁, ВМ₂ и СМ₃ пересекаются в одной точке. Имеем:

Итак, доказано, что медианы треугольника пересекаются в одной точке.

Пусть О – точка пересечения медиан. Прямая М₃С пересекает две стороны треугольника АВМ₂ и продолжение третьей стороны этого треугольника. По теореме Менелая

или .

Рассматривая теорему Менелая для треугольников АМ₁С и АМ₂С, мы получаем, что

. Теорема доказана.

Докажите теорему: Биссектрисы треугольника пересекаются в одной точке. (рисунок 2 слайд 6).

Доказательство: Достаточно показать, что . Тогда по теореме Чевы (обратной) AL_1, BL_2, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника:

. Перемножая почленно полученные равенства, получаем: . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.

Докажите теорему: Высоты остроугольного треугольника пересекаются в одной точке. (рисунок 3 слайд 6).

Доказательство: Пусть АН₁, АН_2, АН₃ – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН₂ и ВСН₂ по теореме Пифагора выразим, соответственно, квадрат общего катета ВН₂, обозначив АН₂ = х, СН₂ = b – х.

Итак, АН₂ = , СН₂ = .

Аналогично рассуждая для прямоугольных треугольников АСН₂ и ВСН₃, ВАН₁ и САН₁, получим АН₃ = , ВН₃ = и ВН₁ = ,

СН₁ = .

Для доказательства теоремы достаточно показать, что . Тогда по теореме Чевы (обратной) отрезки АН₁, ВН₂ и СН₃ пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН₃, ВН₃, ВН₁, СН₁, СН₂ и АН₂ через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.

Задачи 5 – 7 самостоятельное решение 3 учащихся. (чертежи на экране).

2. остальные:

Докажите теорему: Если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон пересекаются в одной точке. (на рисунке 4 слайд 6).

Доказательство: Пусть А₁, В₁ и С₁ – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

. Используя свойство касательных, проведенных из одной точки, введем обозначения: ВС₁ = ВА₁ = х, СА₁ = СВ₁ = у, АВ₁ = АС₁ = z.

. Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в одной точке. Эту точку называют точкой Жергона. Теорема доказана.

3. Разбор задач 5, 6, 7.

Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников. (на слайде 7 рисунок 1)

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то = . По теореме Менелая для треугольника ADC и секущей РВ имеем: . Итак, = .

В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А₁ и С₁ – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА₁ и СС₁. Точка Р лежит на биссектрисе ВВ₁. Найдите АР : РА₁.

(на слайде 7 рисунок 2)

Решение: Точка касания окружности со стороной АС не совпадает с В₁, так как треугольник АВС – разносторонний. Пусть С₁В = х, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см рисунок) 8 – х + 5 – х = 4, х = .

В треугольнике АВА₁ прямая С₁С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая .

Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник. (на слайде 7).

Решение: Пусть в треугольнике АВС АВ = 5, ВС = 7, АС = 6. Угол ВАС лежит против большей стороны в треугольнике АВС, значит, угол ВАС – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О – точка пересечения биссектрис. Необходимо найти АО : ОD. Так как АD – биссектриса треугольника АВС, то , то есть BD = 5k, DС = 6k. так как BF – биссектриса треугольника АВС, то , то есть AF = 5m, FC = 7m. Прямая BF пересекает две стороны и продолжение третьей стороны треугольника ADC. По теореме Менелая .

4. Самостоятельное решение задач 9, 10, 11. – 3 учащихся.

Задача 12 (для всех оставшихся учащихся класса):

Биссектрисы ВЕ и АD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если площадь треугольника BQD = 1, 2АС = 3 АВ, 3ВС = 4 АВ. (рисунок 4 на слайде 7).

Треугольники АВС и ВЕС имеют равные высоты, проведенные из вершины В, значит, , тогда S_ABC = _.

5. Разбор задач 9, 10, 11.

Решение задач – практикум:

А. На сторонах ВС, СА, АВ равнобедренного треугольника АВС с основанием АВ взяты точки А_1, В₁, С_1, так что прямые АА₁, ВВ₁, СС₁ – конкурентные.

Докажите, что

По теореме Чевы имеем: (1 ).

.

Что и требовалось доказать.

По теореме Менелая для треугольника АВС и секущей MN имеем:

. По условию следовательно ,

Для треугольника MNC и секущей АВ по теореме Менелая имеем: по условию

8. Самостоятельное решение задач: 1 вариант:

1. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что АВ = ВС₁, ВС = СА₁, СА = АВ₁. Найдите отношение в котором прямая АВ₁ делит сторону А₁С₁ треугольника А₁В₁С₁. (3 балла).

2. На медиане СС₁ треугольника АВС взята точка М. Прямые АМ и ВМ пересекают стороны треугольника соответственно в точках А₁ и В₁. Докажите, что прямые АВ и А₁В₁ параллельны. (3 балла).

3. Пусть на продолжении сторон АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В_1. Докажите, что точки А₁, В_1, С₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁ так, что прямые АА₁, ВВ₁, СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

1. Точки А₁ и В₁ делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА₁ и ВВ₁ пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС. (3 балла).

2. Отрезок МN, соединяющий середины сторон АD и ВС четырехугольника АВСD делится диагоналями на три равные части. Докажите, что АВСD – трапеция, одно из оснований АВ или СD, которое в двое больше другого. (3 балла).

3. Пусть на стороне АВ и продолжении сторон ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁. Докажите, что прямые АА₁, ВВ₁, СС₁ пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что прямые АА₁, ВВ₁ и СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

9. Домашнее задание: учебник § 3, № 855, № 861, № 859.

Источник