С помощью чего определяют оптимальное количество интервалов при построении гистограммы
Построение гистограмм



1. Определяется наибольшее А и наименьшее В значение показателя.
2. Определяют число интервалов (участков). Обычно оно соответствует корню квадратному из числа данных. При числе данных 100 количество участков равно 10.
4. Значения границ участков определяют следующим образом:
5. Определение центральных значений для первого участка производится по половине суммы граничных значений данного участка: 5,05 + 5,45 / 2 = 5,25. Центральные значения последующих участков находятся прибавлением к значению первого участка 5,25 ширины участка = 0,4.
6. На основании полученных данных составляется Таблица 15.3.
Таблица 15.3. Исходные данные для составления гистограммы
Поскольку гистограмма выражает определенные зависимости, важную информацию может дать форма распределения гистограммы в сравнении с контрольными нормативами. Различают следующие формы гистограммы:
1. Гистограмма с двусторонней симметрией (по закону нормального распределения) встречается чаще всего и указывает на стабильность процесса.
3. Форму, вытянутую влево, гистограмма принимает в случае, когда невозможно получить значения выше определенного.
4. Двугорбая гистограмма содержит два возвышения (которые имеют чаще всего разную высоту) с провалом между ними. Она отражает случаи распределений с разными средними значениями (разницы между двумя станками или сменами, двумя материалами, двумя операторами и т.п.).
5. Гистограмма, не имеющая высокой центральной части, получается в случаях, когда объединяются несколько распределений, средние значения которых имеют небольшую разницу между собой.
Реже, но встречаются гистограммы с обрывом с обеих или с одной стороны (когда исключаются параметры, резко выходящие за границы измерений), гистограммы с прогалом («вырванным зубом»), когда оператор ошибается в считывании показателей.
На гистограммах легко отметить допустимые граничные измерения. Это может быть сделано на основе нормативных значений параметра (из нормативной документации) или путем расчета абсолютной (гарантийной) ошибки опыта.
Алгоритм построения гистограммы



1. Ранжируем вариационный ряд с помощью команды Сортировка на вкладке Главная в группе Редактирование и определяем максимальное 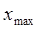
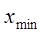
2. Определяем размах выборки по формуле 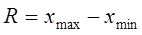
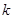
Таб.2 Количество интервалов по объему выборки
| n | 15-20 | 25-30 | 35-60 | 65-100 |
| k |
3. Так как интервалы значений должны быть приблизительно одинаковые, то длина каждого интервала (шаг) вычисляется по формуле 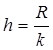
4. Вычисляем границы интервалов по схеме:
| № п/п | Границы интервала |
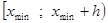 | |
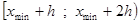 | |
| …. | ………….. |
| k | 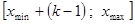 |
5. Высоту прямоугольников определяет накопленная частота 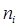
6. Далее вычисляется относительная накопленная частота (частость) для каждого промежутка по формуле 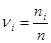
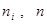
| № п/п | Границы интервала | 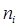 | 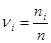 |
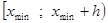 | 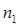 | 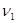 | |
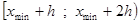 | 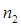 | 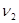 | |
| …. | ………….. | ….. | ….. |
| k | 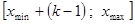 | 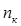 | 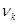 |
7. Последним шагом будет построение гистограммы наблюдения с помощью Гистограммы в группе Гистограммы на вкладке Вставка.
Применим описанный алгоритм к решению нашей задачи.
a) Ранжируем ряд и находим размах выборки
b) Вычисляем количество интервалов при объеме равном 50 и величину шага
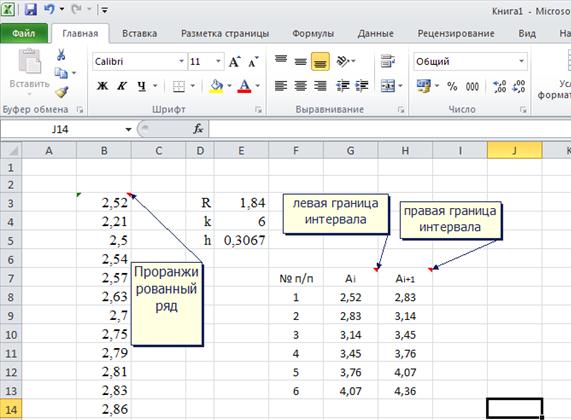
c) Определяем границы интервалов согласно схеме п.4 алгоритма построения гистограммы
Рис. 8 Определение границ интервалов
d) Следующим этапом будет определение накопленной и относительной частот
Рис.9 Значения накопленных и относительных частот
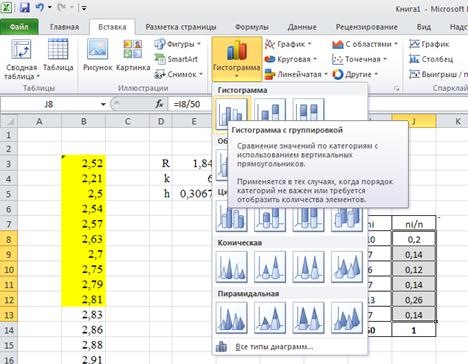
e) Выделяем столбец относительной частоты, строим гистограмму (рис.10а, 10б)
Рис.10а Выбор типа диаграммы
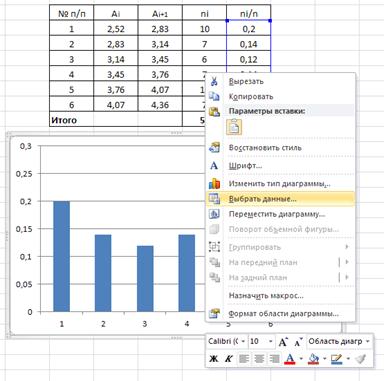
Рис.10б Выбор данных осей координат
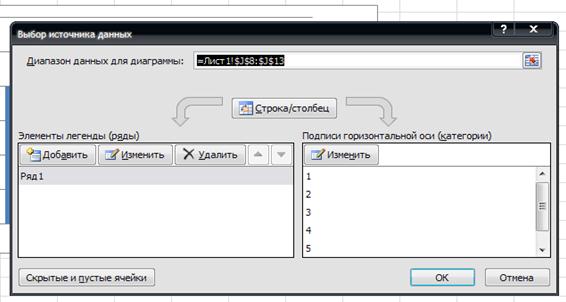
По оси ординат откладываются значения относительных частот, а по оси абсцисс – границы интервалов. Для отоброжения значений границ интервала на гистограмме необходимо активизировать диаграмму щелкнув по ней курсором, правой кнопкой мыши вызвать контекстное меню (см. рис.10б) и выбрать раздел Выбрать данные…В открывшемся диалоговом окне Выбор источника данных изменить подписи горизонтальной оси.
Рис. 11а Определение подписи осей
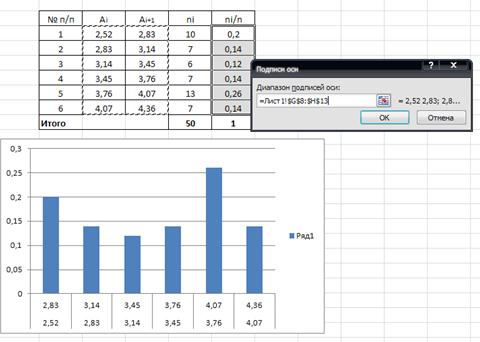
С помощью кнопки Изменить вводим данные границ интервалов (см.рис.11а)
Рис. 11а Определение подписей осей гистограммы



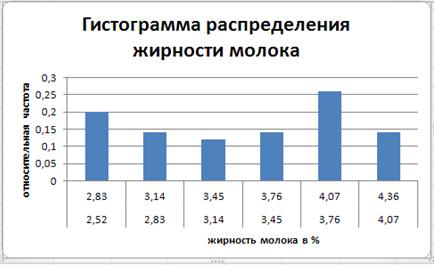
Примерный итоговый результат представлен на рис.11б
Рис.11б Гистограмма результатов проверки жирности молока коров.
Наибольшую высоту имеет интервал номер 5, который является в данном случае модой распределения. Само значение моды в случае непрерывного типа исследуемого признака определяется по формуле 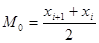
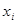
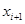
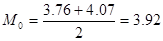
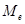
Среднее выборочное определяется по формуле
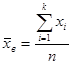
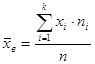
Где 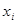
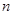
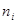
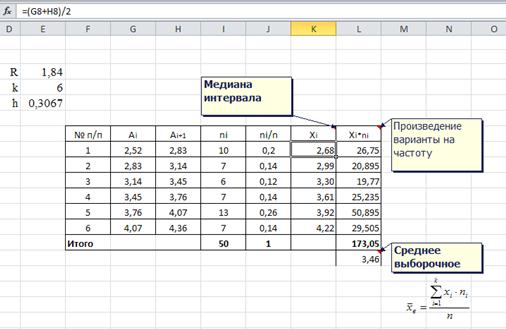
Рассмотрим вычисление среднего выборочного в условиях предыдущей задачи. Разложим формулу 1 по действиям и поместим результат в таблицу.
Рис. 12 Разложение формулы по столбцам
В случае с дискретным признаком берется конкретное значение варианты.
Кроме среднего выборочного еще одной числовой характеристикой вариационного ряда является выборочная дисперсия. Она показывает средний квадрат отклонения данных вариационного ряда от его среднего значения (мера рассеяния).
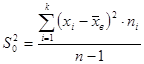
Где 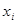
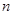
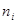
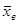
Для удобства поместим все вычисления в таблицу
| № п/п | Ai | Ai+1 | ni | Xi | Xi*ni | Xi-Xв | (Xi-Xв)^2 | (Xi-Xв)^2*ni |
| 2,52 | 2,83 | 2,68 | 26,75 | -0,79 | 0,62 | 6,18 | ||
| 2,83 | 3,14 | 2,99 | 20,895 | -0,48 | 0,23 | 1,59 | ||
| 3,14 | 3,45 | 3,30 | 19,77 | -0,17 | 0,03 | 0,17 | ||
| 3,45 | 3,76 | 3,61 | 25,235 | 0,14 | 0,02 | 0,15 | ||
| 3,76 | 4,07 | 3,92 | 50,895 | 0,45 | 0,21 | 2,68 | ||
| 4,07 | 4,36 | 4,22 | 29,505 | 0,75 | 0,57 | 3,98 | ||
| Итого | 173,05 | 14,73 |
Подставим полученные данные в формулу для выборочной дисперсии (2)
Ещё одной характеристикой меры рассеяния является среднеквадратичное отклонение, которое находится по формуле (3)
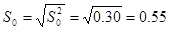
Данная величина показывает, что наибольшее количество значений лежит в интервале от 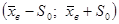
Кроме точечных оценок существуют интервальные оценки истинного параметра распределения.
Интервальная оценка – доверительный интервал 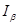
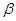
Где 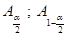
(см. табл.3).
Ниже приводится таблица для построения интервальной оценки параметра распределения.
Табл. 3 Построение интервальной оценки
| Параметр | Интервальная оценка | |
| Математическое ожидание | ( 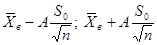 ) ) | Среднее выборочное 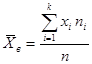 ; Распределение Стьюдента А= ; Распределение Стьюдента А= 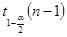 — если — если 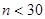 Стандартное нормальное распределение А= Стандартное нормальное распределение А= 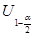 — если — если 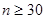 ; ; 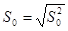 — среднеквадратическое отклонение — среднеквадратическое отклонение |
| Дисперсия | ( 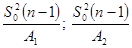 ) ) | Выборочная дисперсия 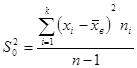 ; Распределение Хи-квадрат ; Распределение Хи-квадрат 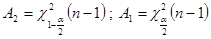 |
| Доля признака | 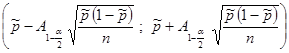 | Стандартное нормальное распределение А= 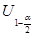 ; ; 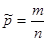 — выборочная доля признака; — выборочная доля признака; 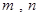 — число благоприятных и всевозможных исходов соответственно — число благоприятных и всевозможных исходов соответственно |
5. По заданному значению среднего квадратичного отклонения нормально распределенной случайной величины равным 9, с выборочным средним 18,31 и объемом выборки в 49 элементов построить доверительный интервал для математического ожидания с заданной надежностью 0,95.
Запишем данные задачи математическим языком
Дано: 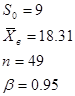 | Решение 1). Т.к. интервал необходимо построить для математического ожидания и выборка малого объема 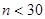 , то воспользуемся следующей формулой ( , то воспользуемся следующей формулой ( 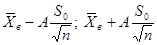 ), где А= ), где А= 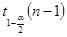 — квантиль распределения Стьюдента. — квантиль распределения Стьюдента. |
2). Значения квантилей зависит от уровня значимости 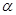
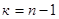
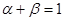
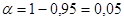
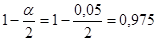
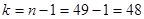
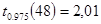
3). Подставляем числовые значения в формулу доверительного интервала для математического ожидания
4). Полученный результат означает, что с вероятность 97,5 % истинное значение параметра будет лежать в этом интервале. Изменяя уровень значимости интервальная оценка будет меняться.
6. Результаты 10 независимых измерений длины стержня (мм): 32, 35, 33, 34, 33, 32, 36, 36, 32, 35. Построить доверительный интервал для дисперсии с доверительной вероятностью 0,95.
Дано: 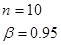 | Решение 1). Доверительный интервал для дисперсии строится по формуле ( 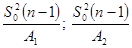 ), где ), где 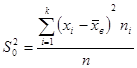 — выборочная дисперсия; — выборочная дисперсия; 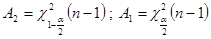 -квантили распределение Хи-квадрат. -квантили распределение Хи-квадрат. |
2). Так же как квантили распределения Стьюдента значения квантилей Хи-квадрат зависят от уровня значимости 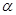
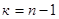
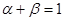
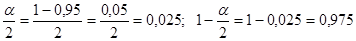
Число степеней свободы равно 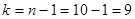
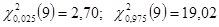
3). В условии задания нет значения выборочной дисперсии, но есть результаты измерений длины стержня, которые образуют выборку малого объема. Определим точечную оценку дисперсии, результат вычислений представим в виде таблицы
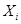 | 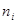 | 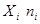 | 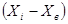 | 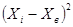 | 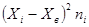 |
| -1,8 | 3,24 | 9,72 | |||
| -0,8 | 0,64 | 1,28 | |||
| 0,2 | 0,04 | 0,04 | |||
| 1,2 | 1,44 | 2,88 | |||
| 2,2 | 4,84 | 9,68 | |||
| Итого | 23,6 |
Итоговый результат: среднее выборочное 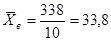
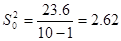
4). С вероятность 97,5 % интервал накрывает истинное значение параметра.
Дано:  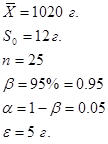 | Решение: Выборка, произведенная специалистом, маленькая ( 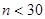 ), поэтому определим квантиль распределения Стьюдента с вероятностью ), поэтому определим квантиль распределения Стьюдента с вероятностью 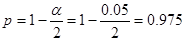 и числом степеней свободы и числом степеней свободы 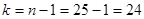 , по таблице квантилей t-распределения (приложение 1) определяем , по таблице квантилей t-распределения (приложение 1) определяем |
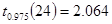
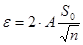
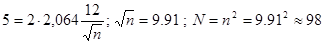
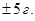
Примечание. Если выборка большая, объем 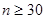
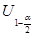
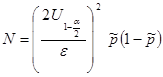
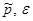
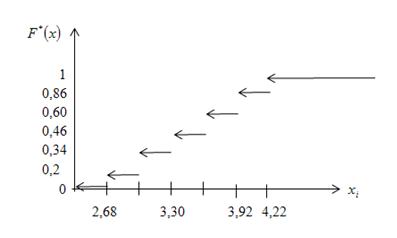
8. Требуется составить эмпирическую функцию распределения группированной выборки (см. условие задачи 4) и построить ее график.
Значения эмпирической функции распределения для статистики определяются следующим образом
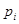
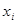
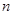
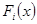
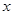
Воспользуемся группировкой произведенной в задаче 4
| № п/п | 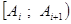 | 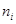 | 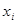 | 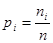 | 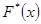 |
| 2,52 | 2,83 | 2,68 | 0,20 | ||
| 2,83 | 3,14 | 2,99 | 0,14 | 0,20 | |
| 3,14 | 3,45 | 3,30 | 0,12 | 0,34 | |
| 3,45 | 3,76 | 3,61 | 0,14 | 0,46 | |
| 3,76 | 4,07 | 3,92 | 0,26 | 0,60 | |
| 4,07 | 4,36 | 4,22 | 0,14 | 0,86 | |
| Итого |
Рис. 13 График эмпирической функции распределения
9. Компания, выпускающая в продажу новый сорт кофе, провела проверку вкусов покупателей по случайной выборке из 400 человек и выяснила, что 220 из них предпочли новый сорт всем остальным. Проверьте на уровне значимости
α = 0,01 гипотезу о том, что, по крайней мере, 52% потребителей предпочтут новый сорт кофе.
Статистическая гипотеза – предположение о генеральной совокупности, которое проверяют по выборочной совокупности (по результатам наблюдений).
Проверка гипотезы – с помощью определенных правил высказанную гипотезу сопоставляют с выборочными данными и делают вывод о том, можно принять гипотезу или нет.
Рассмотрим этапы проверки гипотезы.
1 этап. По выборочным данным и руководствуясь конкретными условиями задачи, формулируем гипотезы 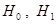
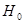
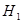
— по выборке принимается решение о справедливости для генеральной совокупности гипотезы 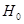
— по выборке принимается решение о справедливости для генеральной совокупности гипотезы 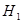
2 этап. Задается вероятность 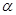
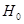
| Верная гипотеза | Принимается | |
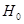 | 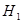 | |
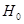 | — | Ошибка первого рода; 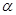 — вероятность ошибки — вероятность ошибки |
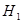 | Ошибка второго рода; 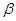 — вероятность ошибки — вероятность ошибки | — |
Поскольку проверка осуществляется относительно основной гипотезы, то ее вероятность 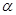
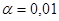
3 этап. Определяют величину К – статистику такую, что
— ее значения зависят от выборочных данных;
— величина К подчиняется некоторому известному закону распределения при выполнении основной гипотезы 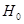
— ее значения позволяют судить о расхождении гипотезы 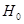
В зависимости от формулировки основной гипотезы используют следующие статистики и законы распределения (см. табл.)
| Величина | Статистика (К) | Закон |
Математическое ожидание 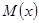 | 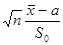 | Распределение Стьюдента 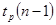 — если — если 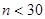 Стандартное нормальное распределение Стандартное нормальное распределение 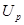 — если — если 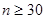 |
| Доля признака p | 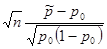 | Стандартное нормальное распределение 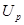 — если — если 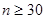 |
Дисперсия 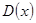 | 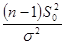 | Распределение Хи-квадрат 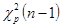 |
Разность долей признака 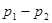 | 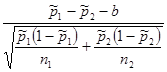 | Стандартное нормальное распределение 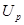 |
Где n – объем выборки, 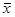
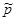
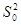
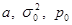
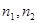
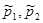
4 этап. В области всевозможных значений статистики К выделяют критическую область. Значения критерия, попавшие в эту подобласть, свидетельствуют о существенном расхождении выборки с гипотезой 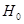
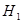
Данному требованию удовлетворяют три случая расположения критической области (в зависимости от вида нулевой и альтернативной гипотез, формы и распределения статистики).
| Вид критической области | Характерные черты | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
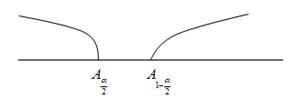
Правосторонняя 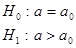 | Состоит из интервала 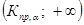  область допустимых значений ( область допустимых значений ( 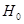 ) ( ) ( 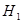 ) критическая область ) критическая область  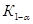 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Левосторонняя 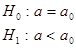 | 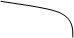 Состоит из интервала Состоит из интервала 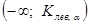 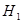 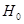  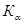 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Двухсторонняя 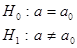 | Состоит из двух интервалов 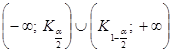
5 этап. Согласно формуле статистики, которая вычисляется в зависимости от формулировки основной гипотезы, находят числовое значение критерия Если
2). Альтернативная гипотеза правосторонняя, квантиль, определяющий границу критической области, находится из таблицы квантилей нормального стандартного распределения с вероятностью 3). Сравниваем табличное значение с найденной статистикой получаем 4). Предположение о том, что, по крайней мере, 52 % потребителей предпочтут новый сорт кофе на уровне значимости 1 % подтверждается. 10. Для данной выборки с помощью критерия Пирсона проверить гипотезу о нормальном виде распределения генеральной совокупности на уровне значимости 5 %.
1. Рассматриваемые величины относятся к непрерывному типу выборки, для ее графического представления необходимо произвести группировку данных (см. зад.4). После необходимых операций результат выглядит следующим образом
При этом в качестве варианты берется значение медианы каждого промежутка По условию задачи необходимо проверить гипотезу о нормальном распределении Для определения близости найдем теоретические частоты
Значения 5 колонки определяется по таблице Приложения 2, где Рис.14 Аргументы функции НОРМРАСП Теоретическая частота
Итак, статистика критерия равна 12,48. Определяем значение границы критической области: число степеней свободы
|



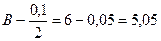
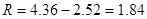
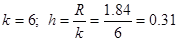


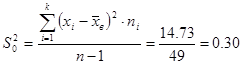
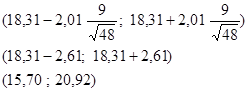
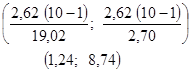
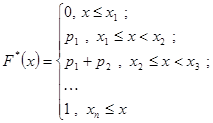



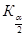
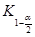
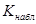 по выборочным данным.
по выборочным данным.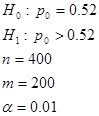
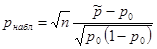 , где
, где 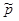 — оценка доли признака,
— оценка доли признака, 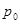 — предполагаемое значение параметра. (см. табл.). Оценка доли признака равна отношению числа благоприятных исходов
— предполагаемое значение параметра. (см. табл.). Оценка доли признака равна отношению числа благоприятных исходов 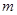 к числу всевозможных
к числу всевозможных 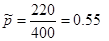 , отсюда
, отсюда 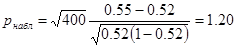
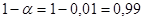 . По таблице Приложения 3 или через функцию НОРМ.СТ.ОБР Microsoft Excel находим
. По таблице Приложения 3 или через функцию НОРМ.СТ.ОБР Microsoft Excel находим 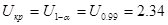
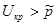 , т.е. нет оснований отклонять основную гипотезу.
, т.е. нет оснований отклонять основную гипотезу.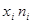
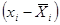
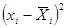
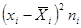
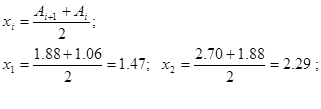 и т.д. Среднее выборочное значение получается из суммы значений 5 столбца деленной на объем выборки (итог третьей колонки)
и т.д. Среднее выборочное значение получается из суммы значений 5 столбца деленной на объем выборки (итог третьей колонки) 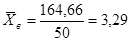 . Среднеквадратическое отклонение равно
. Среднеквадратическое отклонение равно 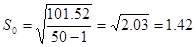 .
.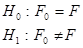 , т.е. основная гипотеза – распределения похожи, альтернативная – сходства между распределениями нет. Статистика критерия определяется по формуле
, т.е. основная гипотеза – распределения похожи, альтернативная – сходства между распределениями нет. Статистика критерия определяется по формуле 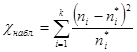 , где
, где 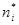 — теоретическая частота,
— теоретическая частота, 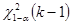 .
.

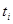
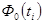
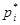
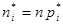
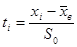 , либо с помощью функции НОРМРАСП Microsoft Excel
, либо с помощью функции НОРМРАСП Microsoft Excel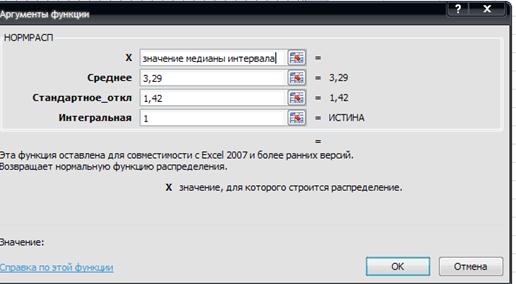
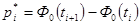 . Условие применения критерия Пирсона
. Условие применения критерия Пирсона 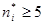 , т.е. значения теоретических частот должно быть больше либо равное 5. В противном случае, группы с меньшими частотами объединяем с соседними, до тех пор пока не получим необходимое значение, при этом не забываем о наблюдаемой частоте объединяемых интервалов. Представим в виде таблицы вычисления статистики критерия
, т.е. значения теоретических частот должно быть больше либо равное 5. В противном случае, группы с меньшими частотами объединяем с соседними, до тех пор пока не получим необходимое значение, при этом не забываем о наблюдаемой частоте объединяемых интервалов. Представим в виде таблицы вычисления статистики критерия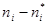
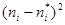
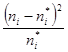
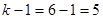 ; вероятность
; вероятность 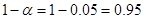 , по таблице Приложения 4 или с помощью функции ХИ2.ОБР находим его значение
, по таблице Приложения 4 или с помощью функции ХИ2.ОБР находим его значение 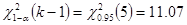 . Сравнивая данный показатель со значением статистики видим, что 11,07
. Сравнивая данный показатель со значением статистики видим, что 11,07