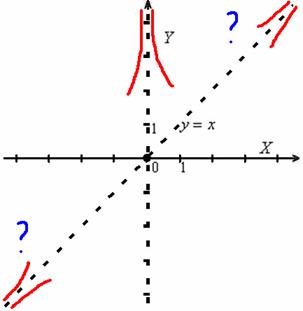
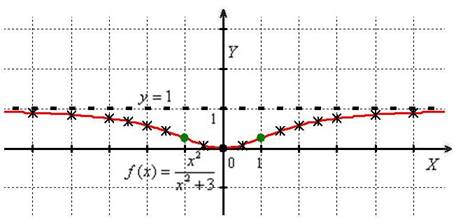
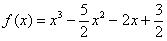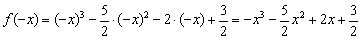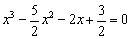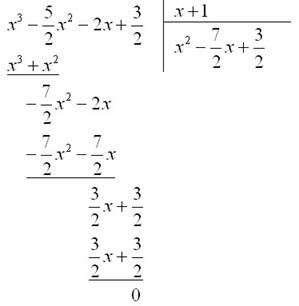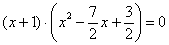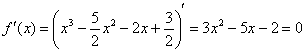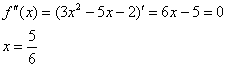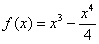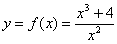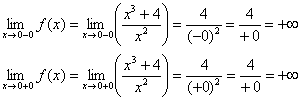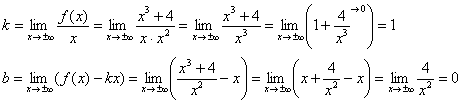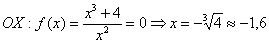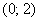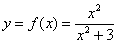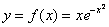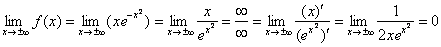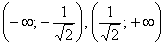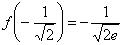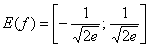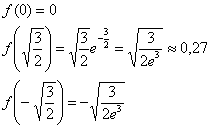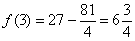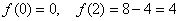С чего начинается график функции

Построение графиков функций

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При значение cos x равно единице. Значение функции в этих точках будет равно при

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при при

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции:

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Источник

с чего начинается график функции)

В Кемерово бастуют сборщики Яндекс.Еды — заказы лучше не делать

В Кемерово бастуют сборщики Яндекс.Еды — предупреждаем жителей, что получить свои заказы сегодня и, возможно, в ближайшие дни, будет проблематично.

Как рассказал нашей редакции один из лидеров забастовки, Никита Булынцев, с сегодняшнего дня бастует большая часть сборщиков по Кемерово. Они не намерены работать до тех пор, пока московское руководство не выйдет с ними на связь.

О забастовке предупреждали заранее — участники надеялись, что Яндекс выйдет на контакт, но реакции не было.

«На данный момент спрос по сборке заказов возрос, у нас больше 30 заказов за день, 10-40 позиций. На точке чаще всего работает один человек, который не может присесть, отдохнуть, даже свой 20-минутный перерыв, который положен за 12 часов работы, он не может взять, потому что точка будет остановлена, и человек получит выговор. Мы хотим, чтобы нам ввели бонусы, которые есть во многих регионах — за количество, качество и скорость сборки, тогда наша зарплата вырастет. Потому что, повторюсь, спрос вырос, а зарплата не меняется. Сегодня первый день, точки не будут принимать заказы. На второй день, если начальство не выйдет с нами на связь, мы сделаем немного по-другому… и так до тех пор, пока не начнут переговоры. Если же нас будут увольнять либо отменять наши слоты, мы будем делать публичные посты», — сказал нашему каналу Никита.

Ранее сборщики рассказывали, что устанавливаемый максимум 45 минут на заказ в приложении оборачивается иногда сбором в течении часа из-за большого количества позиций, а значит, расчет приложения неадекватен реальной работе.

«Не знаем, как в других городах, но в Кемерово, обещанные бонусы при устройстве на работу мы не видим. Получаем только минималку. Курьеры, которые развозят наши заказы в размере 20 штук за смену, они получают свыше 5 тысяч рублей. Наша зарплата более чем в три раза меньше», — говорили они.

«Я прекрасно понимаю, что буду уволен. Главное, чтобы ребятам ставку подняли», — сказал нашему каналу Никита Булынцев

Давайте следить за происходящим вместе в тг-канале независимых журналистов из Новосибирска @сибирьмедиа. Пишем о несправедливостях, поддерживаем хорошее, отмечаем смешное, анализируем страшное

Источник

График линейной функции, его свойства и формулы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Свойства линейной функции

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Точки пересечения графика функции y = kx + b с осями координат:

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Источник

Как исследовать функцию и построить её график?

Похоже, я начинаю понимать одухотворённо-проникновенный лик вождя мирового пролетариата, автора собрания сочинений в 55 томах…. Нескорый путь начался элементарными сведениями о функциях и графиках, и вот сейчас работа над трудоемкой темой заканчивается закономерным результатом – статьёй о полном исследовании функции. Долгожданное задание формулируется следующим образом:

Исследовать функцию методами дифференциального исчисления и на основании результатов исследования построить её график

Или короче: исследовать функцию и построить график.

Зачем исследовать? В простых случаях нас не затруднит разобраться с элементарными функциями, начертить график, полученный с помощью элементарных геометрических преобразований и т.п. Однако свойства и графические изображения более сложных функций далеко не очевидны, именно поэтому и необходимо целое исследование.

Основные этапы решения сведены в справочном материале Схема исследования функции, это ваш путеводитель по разделу. Чайникам требуется пошаговое объяснение темы, некоторые читатели не знают с чего начать и как организовать исследование, а продвинутым студентам, возможно, будут интересны лишь некоторые моменты. Но кем бы вы ни были, уважаемый посетитель, предложенный конспект с указателями на различные уроки в кратчайший срок сориентирует и направит Вас в интересующем направлении. Роботы прослезились =) Руководство свёрстано в виде pdf-файла и заняло заслуженное место на странице Математические формулы и таблицы.

Исследование функции я привык разбивать на 5-6 пунктов:

1) Область определения, непрерывность, четность/нечётность, периодичность функции.

2) Асимптоты графика функции.

6) Дополнительные точки и график по результатам исследования.

На счёт заключительного действия, думаю, всем всё понятно – будет очень обидно, если в считанные секунды его перечеркнут и вернут задание на доработку. ПРАВИЛЬНЫЙ И АККУРАТНЫЙ ЧЕРТЁЖ – это основной результат решения! Он с большой вероятностью «прикроет» аналитические оплошности, в то время как некорректный и/или небрежный график доставит проблемы даже при идеально проведённом исследовании.

Следует отметить, что в других источниках количество пунктов исследования, порядок их выполнения и стиль оформления могут существенно отличаться от предложенной мной схемы, но в большинстве случаев её вполне достаточно. Простейшая версия задачи состоит всего из 2-3 этапов и формулируется примерно так: «исследовать функцию с помощью производной и построить график» либо «исследовать функцию с помощью 1-й и 2-й производной, построить график».

Естественно – если в вашей методичке подробно разобран другой алгоритм или ваш преподаватель строго требует придерживаться его лекций, то придётся внести некоторые коррективы в решение. Не сложнее, чем заменить вилку бензопилой ложкой.

Итак, вооружившись общей схемой исследования, где рассмотрена структура и техника выполнения задачи, переходим к изучению стратегии и тактики действий. Успешно прошедшим курс обучения откроется тайна числа 69 😉 С нетерпением скрипим колёсиком мыши =)

Исследовать функцию и по результатам исследования построить график.

Решение:
1) Функция определена и непрерывна на всей числовой прямой: 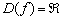. Это очень хорошо, отпадают вертикальные асимптоты.

Проверим функцию на чётность/нечётность:

После чего следует шаблонная отписка: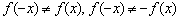
, значит, данная функция не является чётной или нечётной.

Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.

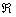
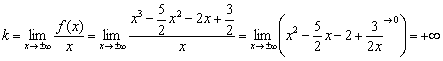
Так как функция непрерывна на , то вертикальные асимптоты отсутствуют.

Нет и наклонных асимптот.

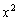
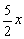
Примечание: напоминаю, что более высокого порядка роста, чем , поэтому итоговый предел равен именно «плюс бесконечности».

Выясним, как ведёт себя функция на бесконечности:

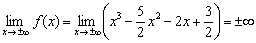
Иными словами, если идём вправо, то график уходит бесконечно далеко вверх, если влево – бесконечно далеко вниз. Да, здесь тоже два предела под единой записью. Если у вас возникли трудности с расшифровкой знаков 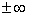, пожалуйста, посетите урок о бесконечно малых функциях.

Таким образом, функция не ограничена сверху и не ограничена снизу. Учитывая, что у нас нет точек разрыва, становится понятна и область значений функции: 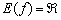– тоже любое действительное число.

ПОЛЕЗНЫЙ ТЕХНИЧЕСКИЙ ПРИЁМ

Каждый этап задания приносит новую информацию о графике функции, поэтому в ходе решения удобно использовать своеобразный МАКЕТ. Изобразим на черновике декартову систему координат. Что уже точно известно? Во-первых, у графика нет асимптот, следовательно, прямые чертить не нужно. Во-вторых, мы знаем, как функция ведёт себя на бесконечности. Согласно проведённому анализу, нарисуем первое приближение: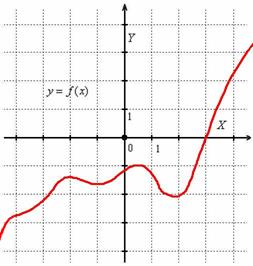

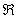
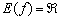
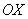
Заметьте, что в силу непрерывности функции на и того факта, что , график должен, по меньшей мере, один раз пересечь ось . А может быть точек пересечения несколько?

3) Нули функции и интервалы знакопостоянства.

Сначала найдём точку пересечения графика с осью ординат. Это просто. Необходимо вычислить значение функции при :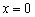

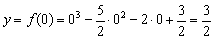
Полтора над уровнем моря.

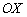
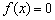
Чтобы найти точки пересечения с осью (нули функции) требуется решить уравнение , и тут нас поджидает неприятный сюрприз:

В конце притаился свободный член, который существенно затрудняет задачу.

Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален. В худшей же сказке нас поджидают три поросёнка. Уравнение разрешимо с помощью так называемых формул Кардано, но порча бумаги сопоставима чуть ли не со всем исследованием. В этой связи разумнее устно либо на черновике попытаться подобрать хотя бы один целый корень. Проверим, не являются ли оными числа :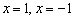
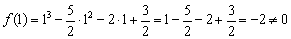
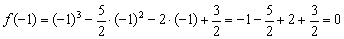
– не подходит;
– есть!

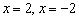
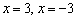
Здесь повезло. В случае неудачи можно протестировать ещё и , а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут пробиваться дополнительные точки. И если таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.

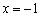
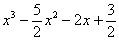
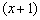
Однако у нас есть красивый корень , поэтому делим многочлен на без остатка:

Алгоритм деления многочлена на многочлен детально разобран в первом примере урока Сложные пределы.

В итоге левая часть исходного уравнения 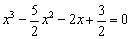раскладывается в произведение:

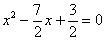
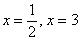
А теперь немного о здоровом образе жизни. Я, конечно же, понимаю, что квадратные уравнения нужно решать каждый день, но сегодня сделаем исключение: уравнение имеет два действительных корня .

На числовой прямой отложим найденные значения 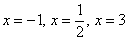и методом интервалов определим знаки функции:

Таким образом, на интервалах 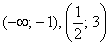график расположен
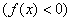
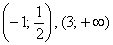
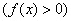
ниже оси абсцисс , а на интервалах – выше данной оси .

Полученные выводы позволяют детализировать наш макет, и второе приближение графика выглядит следующим образом: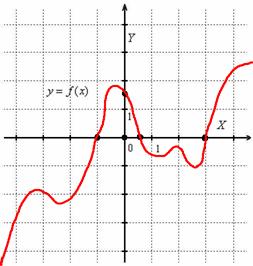

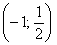
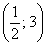
Обратите внимание, что на интервале функция обязательно должна иметь хотя бы один максимум, а на интервале – хотя бы один минимум. Но сколько раз, где и когда будет «петлять» график, мы пока не знаем. К слову, функция может иметь и бесконечно много экстремумов.

4) Возрастание, убывание и экстремумы функции.

Найдём критические точки:

Данное уравнение имеет два действительных корня 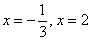. Отложим их на числовой прямой и определим знаки производной:

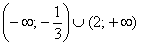
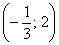
Следовательно, функция возрастает на и убывает на .
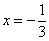
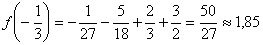
В точке функция достигает максимума: .
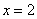
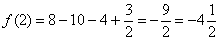
В точке функция достигает минимума: .

Установленные факты загоняют наш шаблон в довольно жёсткие рамки: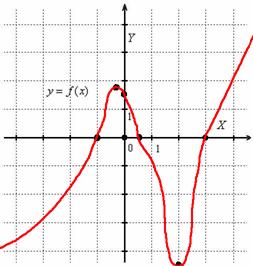

Что и говорить, дифференциальное исчисление – штука мощная. Давайте окончательно разберёмся с формой графика:

5) Выпуклость, вогнутость и точки перегиба.

Найдём критические точки второй производной:

Определим знаки :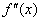

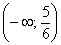
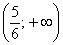
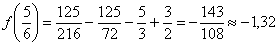
График функции является выпуклым на и вогнутым на . Вычислим ординату точки перегиба: .

Практически всё прояснилось.

6) Осталось найти дополнительные точки, которые помогут точнее построить график и выполнить самопроверку. В данном случае их мало, но пренебрегать не будем:

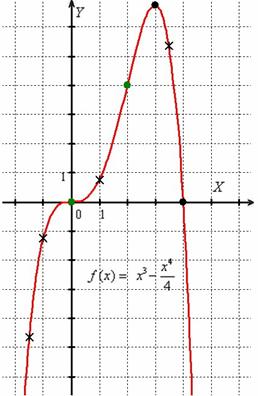
Выполним чертёж: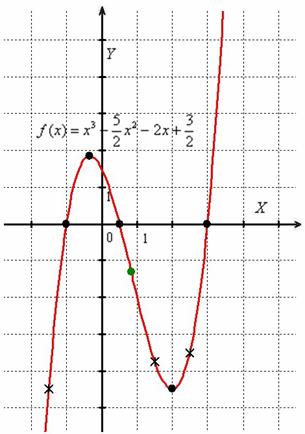

Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.

По ходу выполнения задания я привёл три гипотетических промежуточных чертежа. На практике же достаточно нарисовать систему координат, отмечать найденные точки и после каждого пункта исследования мысленно прикидывать, как может выглядеть график функции. Студентам с хорошим уровнем подготовки не составит труда провести такой анализ исключительно в уме без привлечения черновика.

Для самостоятельного решения:

Исследовать функцию и построить график.

Тут всё быстрее и веселее, примерный образец чистового оформления в конце урока.

Немало секретов раскрывает исследование дробно-рациональных функций:

Методами дифференциального исчисления исследовать функцию и на основании результатов исследования построить её график.

Решение: первый этап исследования не отличается чем-то примечательным, за исключением дырки в области определения:

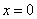
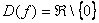
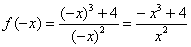
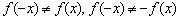
1) Функция определена и непрерывна на всей числовой прямой кроме точки , область определения: .

, значит, данная функция не является четной или нечетной.

Очевидно, что функция непериодическая.

График функции представляет собой две непрерывные ветви, расположенные в левой и правой полуплоскости – это, пожалуй, самый важный вывод 1-го пункта.

2) Асимптоты, поведение функции на бесконечности.

а) С помощью односторонних пределов исследуем поведение функции вблизи подозрительной точки, где явно должна быть вертикальная асимптота:

Действительно, функции терпит бесконечный разрыв в точке ,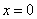
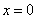
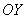
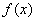
а прямая (ось ) является вертикальной асимптотой графика .

б) Проверим, существуют ли наклонные асимптоты:

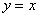
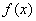
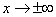
Да, прямая является наклонной асимптотой графика , если .

Пределы 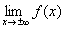анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.

Второй пункт исследования принёс много важной информации о функции. Выполним черновой набросок:

Вывод № 1 касается интервалов знакопостоянства. На «минус бесконечности» график функции однозначно расположен ниже оси абсцисс, а на «плюс бесконечности» – выше данной оси. Кроме того, односторонние пределы сообщили нам, что и слева и справа от точки 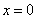функция тоже больше нуля. Обратите внимание, что в левой полуплоскости график, по меньшей мере, один раз обязан пересечь ось абсцисс. В правой полуплоскости нулей функции может и не быть.

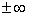
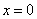
Вывод № 2 состоит в том, что функция возрастает на и слева от точки (идёт «снизу вверх»). Справа же от данной точки – функция убывает (идёт «сверху вниз»). У правой ветви графика непременно должен быть хотя бы один минимум. Слева экстремумы не гарантированы.

Вывод № 3 даёт достоверную информацию о вогнутости графика в окрестности точки 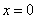. О выпуклости/вогнутости на бесконечностях мы пока ничего сказать не можем, поскольку линия может прижиматься к своей асимптоте как сверху, так и снизу. Вообще говоря, есть аналитический способ выяснить это прямо сейчас, но форма графика «даром» прояснится на более поздних этапах.

Зачем столько слов? Чтобы контролировать последующие пункты исследования и не допустить ошибок! Дальнейшие выкладки не должны противоречить сделанным выводам.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.

График функции не пересекает ось .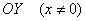

С осью

Методом интервалов определим знаки :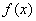

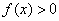
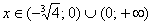
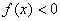
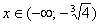
, если ;
, если .

Результаты пункта полностью соответствуют Выводу № 1. После каждого этапа смотрите на черновик, мысленно сверяйтесь с исследованием и дорисовывайте график функции.

4) Возрастание, убывание, экстремумы функции.

В рассматриваемом примере числитель почленно делится на знаменатель, что очень выгодно для дифференцирования: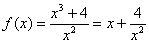

Собственно, это уже проделывалось при нахождении асимптот.

– критическая точка.

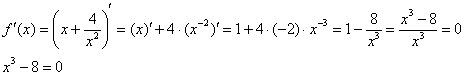
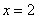
Определим знаки :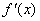

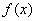
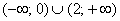
возрастает на и убывает на

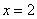
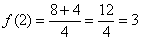
В точке функция достигает минимума: .

Разночтений с Выводом № 2 также не обнаружилось, и, вероятнее всего, мы на правильном пути.

5) Выпуклость, вогнутость, перегибы графика.

, значит, график функции является вогнутым на всей области определения.

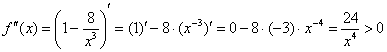
Отлично – и чертить ничего не надо.

Точки перегиба отсутствуют.

Вогнутость согласуется с Выводом № 3, более того, указывает, что на бесконечности (и там и там) график функции расположен выше своей наклонной асимптоты.

6) Добросовестно приколотим задание дополнительными точками. Вот здесь придётся изрядно потрудиться, поскольку из исследования нам известны только две точки.

И картинка, которую, наверное, многие давно представили:

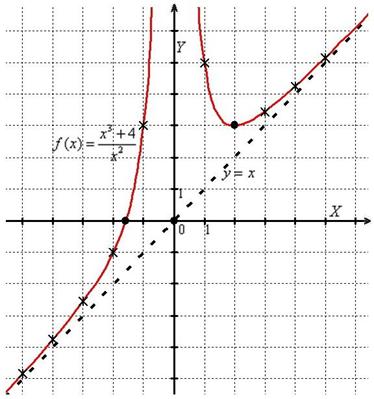
В ходе выполнения задания нужно тщательно следить за тем, чтобы не возникало противоречий между этапами исследования, но иногда ситуация бывает экстренной или даже отчаянно-тупиковой. Вот «не сходится» аналитика – и всё тут. В этом случае рекомендую аварийный приём: находим как можно больше точек, принадлежащих графику (сколько хватит терпения), и отмечаем их на координатной плоскости. Графический анализ найденных значений в большинстве случаев подскажет, где правда, а где ложь. Кроме того, график можно предварительно построить с помощью какой-нибудь программы, например, в том же Экселе (понятно, для этого нужны навыки).

Методами дифференциального исчисления исследовать функцию и построить её график.

Это пример для самостоятельного решения. В нём самоконтроль усиливается чётностью функции – график симметричен относительно оси 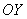, и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.

Чётную или нечётную функцию можно исследовать только при 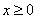, а потом пользоваться симметрией графика. Такое решение оптимально, однако выглядит, по моему мнению, весьма непривычно. Лично я рассматриваю всю числовую ось, но дополнительные точки нахожу всё же лишь справа:

Провести полное исследование функции и построить её график.

Решение: понеслась нелёгкая:

1) Функция определена и непрерывна на всей числовой прямой: .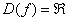

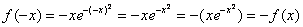
, значит, данная функция является нечетной, её график симметричен относительно начала координат.

Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.

Так как функция непрерывна на 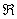, то вертикальные асимптоты отсутствуют

Для функции, содержащей экспоненту, типично раздельное исследование «плюс» и «минус бесконечности», однако нашу жизнь облегчает как раз симметрия графика – либо и слева и справа есть асимптота, либо её нет. Поэтому оба бесконечных предела можно оформить под единой записью. В ходе решения используем правило Лопиталя:

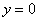
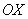
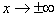
Прямая (ось ) является горизонтальной асимптотой графика при .

Обратите внимание, как я хитро избежал полного алгоритма нахождения наклонной асимптоты: предел 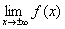вполне легален и проясняет поведение функции на бесконечности, а горизонтальная асимптота обнаружилась «как бы заодно».

Из непрерывности на 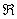и существования горизонтальной асимптоты следует тот факт, что функция ограничена сверху и ограничена снизу.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства.

Здесь тоже сокращаем решение:
График 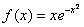проходит через начало координат.

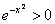
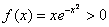
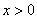
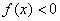
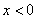
Других точек пересечения с координатными осями нет. Более того, интервалы знакопостоянства очевидны, и ось можно не чертить: , а значит, знак функции зависит только от «икса»:
, если ;
, если .

! Настоятельно рекомендую оформлять черновой шаблон графика
по ходу исследования!

4) Возрастание, убывание, экстремумы функции.

– критические точки.

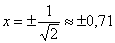
Точки симметричны относительно нуля, как оно и должно быть.

Определим знаки производной:

Функция возрастает на интервале 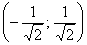и убывает на интервалах

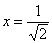
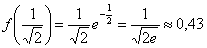
В точке функция достигает максимума: .

В силу свойства 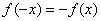(нечётности функции) минимум можно не вычислять:

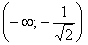
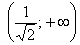
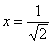
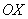
Поскольку функция убывает на интервале , то, очевидно, на «минус бесконечности» график расположен под своей асимптотой. На интервале функция тоже убывает, но здесь всё наоборот – после перехода через точку максимума линия приближается к оси уже сверху.

Из вышесказанного также следует, что график функции является выпуклым на «минус бесконечности» и вогнутым на «плюс бесконечности».

После этого пункта исследования прорисовалась и область значений функции:

Если у вас возникло недопонимание каких-либо моментов, ещё раз призываю начертить в тетради координатные оси и с карандашом в руках заново проанализировать каждый вывод задания.

5) Выпуклость, вогнутость, перегибы графика.

– критические точки.

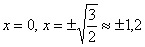
Симметрия точек сохраняется, и, скорее всего, мы не ошибаемся.

Определим знаки :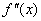

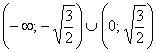
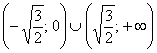
График функции является выпуклым на и вогнутым на .

Выпуклость/вогнутость на крайних интервалах подтвердилась.

Во всех критических точках существуют перегибы графика. Найдём ординаты точек перегиба, при этом снова сократим количество вычислений, используя нечётность функции:

6) Дополнительные точки целесообразно рассчитать только для правой полуплоскости:

Выполним чертёж: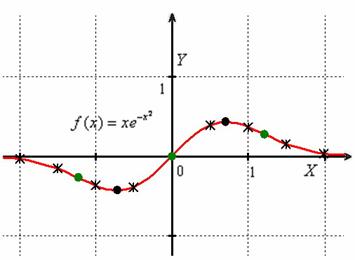

Такой вот симпатяга….

Изначально было запланировано 5 примеров, и если честно, я ожидал, что статья получится заметно больше по объему. Конечно, хочется исследовать ещё одну функцию, но с другой стороны – нельзя объять необъятное, поэтому сегодня воздержимся от логарифмов. Самое важное – усвоить методы, приёмы и хитрости исследования, которые мы только что разобрали.

Желающие могут пройти на страницу готовых задач по высшей математике и закачать архив, который содержит 69 исследований. Выбирайте любую функцию и тренируйтесь! А кто знает…, может встретите ту единственную, которую так давно искали =)

Пример 2: Решение: проведём исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, .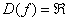

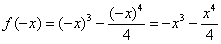
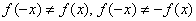
, значит, данная функция не является четной или нечетной.
Функция непериодическая.

2) Асимптоты графика, поведение функции на бесконечности.
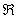
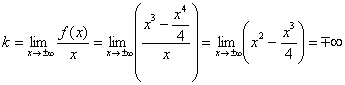
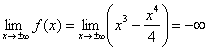
Так как функция непрерывна на , то вертикальные асимптоты отсутствуют.
, значит, наклонные асимптоты также отсутствуют.
, функция не ограничена снизу.

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График 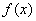проходит через начало координат.
С осью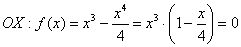

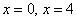
Определим знаки :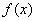

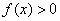
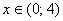
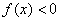
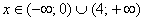
, если ,
, если .

4) Возрастание, убывание, экстремумы функции.

– критические точки.
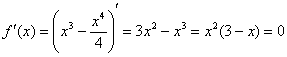
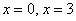
Определим знаки :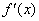

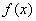
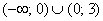
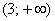
возрастает на и убывает на .
В точке 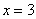функция достигает максимума:

5) Выпуклость, вогнутость, перегибы графика.

– критические точки.
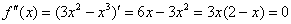
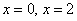
Определим знаки :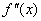

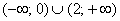
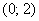
График функции является выпуклым на и вогнутым на .
В обеих критических точках существуют перегибы графика.

6) Найдем дополнительные точки:

Выполним чертёж:

Пример 4: Решение: проведем исследование функции:

1) Функция определена и непрерывна на всей числовой прямой, .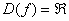

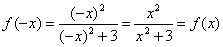
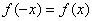
, значит, данная функция является четной, ее график симметричен относительно оси ординат.
Очевидно, что функция непериодическая.

2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на всей числовой прямой, то вертикальные асимптоты отсутствуют.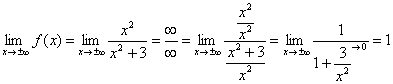

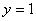
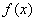
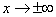
Прямая является горизонтальной асимптотой для графика при .

3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции проходит через начало координат.
на всей области определения.

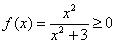
4) Возрастание, убывание, экстремумы функции.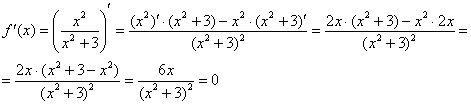

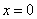
– критическая точка.
Определим знаки :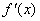

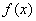
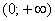
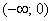
возрастает на и убывает на .
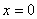
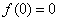
В точке функция достигает минимума: .

5) Выпуклость, вогнутость, перегибы графика.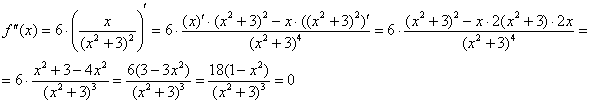

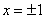
– критические точки.
Определим знаки :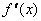

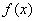
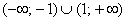
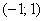
График является выпуклым на и вогнутым на .
В обеих критических точках существуют перегибы графика: .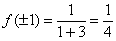

6) Найдем дополнительные точки и выполним чертёж:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

Источник