Рычаг в чем измеряется
Простые механизмы. КПД рычага. Правило рычага.
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
.
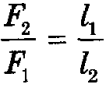
Из формулы 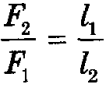, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
Но F1l1 = М1 — момент силы, стремящейся повернуть рычаг по часовой стрелке, a F2l2 = М2 — : момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, М1 =М2, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту 147 м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу 2,5 тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Виды рычагов в физике
Равновесие в физике представляет собой состояние системы, при котором она находится в относительном покое к окружающим объектам. Изучением условий равновесия занимается статика. Одним из механизмов, знание условий равновесия для работы которого имеет принципиальное значение, является рычаг. Рассмотрим в статье, какие виды рычагов бывают.
Что это в физике?
Вам будет интересно: «Несмотря»: как пишется это слово
Вам будет интересно: «Несмотря»: как пишется это слово
Понятие о вращающем моменте
Понимание принципа работы разного вида рычагов в физике возможно, если изучить вопрос равновесия рассматриваемого механизма, которое тесным образом связано с понятием момента силы.
Момент силы обеспечивает возможность совершить поворот вокруг данной оси всей системы. Яркими примерами, в которых можно наблюдать момент силы в действии, являются откручивание гаечным ключом гайки или открывание двери за ручку, находящуюся далеко от дверных петель.
Вращающий момент является векторной величиной. В решении задач часто приходится учитывать его знак. Следует запомнить, что всякая сила, вызывающая вращение системы тел против часовой стрелки, создает момент силы со знаком +.
Равновесие рычага
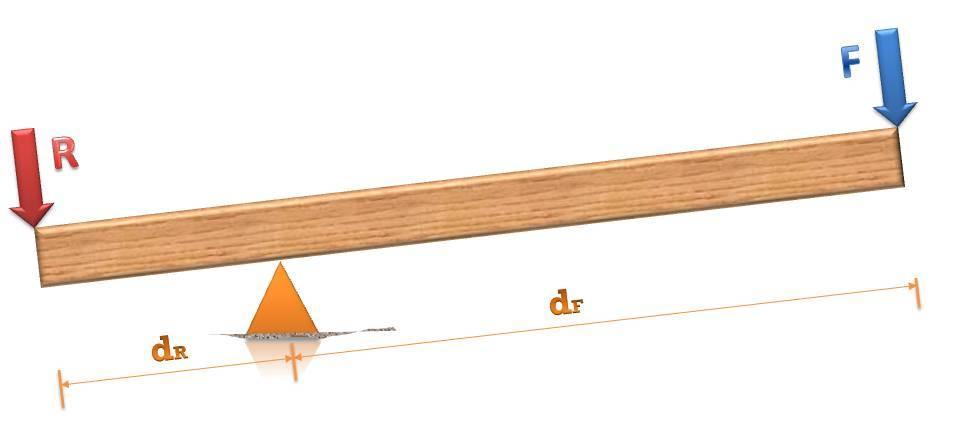
Чтобы рычаг не совершал вращательные движения, необходимо, чтобы сумма всех моментов сил была равна нулю. Плечо силы реакции опоры равно нулю, поэтому момента она не создает. Остается записать моменты сил F и R:
Записанное условие равновесия рычага в виде формулы, также приводится:
Это равенство означает, что для того, чтобы рычаг не совершал вращение, внешняя сила должна быть во столько раз больше (меньше) веса поднимаемого груза, во сколько раз плечо этой силы меньше (больше) плеча, на которое действует вес груза.
Приведенная формулировка означает, что во сколько раз мы выигрываем в пути с помощью рассматриваемого механизма, во столько же раз проигрываем в силе.
Рычаг первого рода
Он был показан в предыдущем пункте. Здесь лишь скажем, что для рычага данного вида опора расположена между действующими силами F и R. В зависимости от соотношения длин плеч такой рычаг может применяться как для подъема тяжестей, так и для придания телу ускорения.
Примерами рычагов первого рода являются механические весы, ножницы, гвоздодер, катапульта.
В случае весов мы имеет два плеча одинаковой длины, поэтому равновесие рычага достигается только в том случае, когда силы F и R равны друг другу. Этот факт используется для взвешивания тел неизвестной массы путем сравнения ее с эталонным значением.
Что касается катапульты, то это яркий пример выигрыша с помощью рычага в пути, а значит, и в ускорении, которое его плечо сообщает снаряду.
Рычаг второго рода
Во всех рычагах второго рода опора находится вблизи одного из концов балки. Это ее расположение приводит к наличию всего одного плеча у рычага. При этом вес груза расположен всегда между опорой и внешней силой F. Расположение сил в рычаге второго рода приводит к единственному полезному результату: выигрышу в силе.
Примерами этого вида рычага являются тачка ручная, которая служит для перевозки тяжелых грузов, а также орехокол. В обоих случаях проигрыш в пути не имеет никакого отрицательного значения. Так, в случае ручной тачки важно лишь удерживать груз на весу во время его перемещения. При этом прилагаемая сила оказывается в несколько раз меньше веса груза.
Рычаг третьего рода
Конструкция рычага этого вида во многом подобна предыдущему. Опора в этом случае также расположена на одном из концов балки, и рычаг обладает единственным плечом. Однако расположение действующих сил в нем совершенно иное, чем в рычаге второго рода. Точка приложения силы F находится между весом груза и опорой.
В заключение отметим, что все виды рычагов работают по одному и тому же принципу. Они не дают выигрыша в работе по перемещению грузов, а лишь позволяют перераспределить эту работу в сторону более удобного ее выполнения.
РЫЧАГ
Смотреть что такое РЫЧАГ в других словарях:
РЫЧАГ
одна из так называемых простых машин. Уже в сочинениях Аристотеля рассматривается действие Р. Действие равноплечих весов он объясняет правильно, предст. смотреть
РЫЧАГ
простейший механизм, позволяющий меньшей силой уравновесить большую; представляет собой твёрдое тело, вращающееся вокруг неподвижной опоры. Осн. смотреть
РЫЧАГ
РЫЧАГ
рычаг м. 1) Твердое тело (обычно стержень), могущее вращаться вокруг неподвижной оси, служащее для уравновешивания большей силы при помощи меньшей и употребляющееся для подъема тяжести. 2) а) Составная часть различных машин, механизмов, обычно в виде стержня, служащая для передачи движения чему-л., управления чем-л. б) Приспособление для соединения и разъединения контактов, обычно в виде стержня с крючком или стержня с двумя развилками, на которые вешается или кладется трубка (в телефонном аппарате).
РЫЧАГ
рычаг м.lever; (перен.) key factor рычаг управления — control lever спусковой рычаг — sear рычаг поворота — steering lever переводной рычаг (стрелки) ж. смотреть
РЫЧАГ
РЫЧАГ
РЫЧАГ, простейший механизм, позволяющий меньшей силой уравновесить большую; представляет- собой твёрдое тело, вращающееся вокруг неподвижной опоры. О. смотреть
РЫЧАГ
Рычаг — одна из так называемых простых машин. Уже в сочинениях Аристотеля рассматривается действие Р. Действие равноплечих весов он объясняет правильно, представляя коромысло современных ему весов, не имевших еще чашек, в виде прямоугольной линейки, подвешенной за середину своей верхней стороны: вертикальная линия, проведенная через точку привеса, делит прямоугольник этот симметрично на две равные части, поэтому он останется горизонтальным сам по себе, и тогда, когда на концы будут положены равные грузы. Если же такое коромысло наклонить, то к поднимающейся его половине прибавится треугольная часть другой половины, перешедшая за вертикальную, проведенную через точку привеса. Вес этого треугольника будет стремиться возвратить коромысло в горизонтальное положение. Если же точка привеса на нижнем конце коромысла, — прибавится вес понизившегося конца и весы не будут возвращаться в прежнее положение. Для случая неравных расстояний от точки опоры, Аристотель лишь высказывает, что приводимый в движение груз относится к проводящему, как обратное отношение их расстояний от точки опоры, утверждая, что движение тем легче происходит, чем груз дальше от точки вращения. Обстоятельнее разбирает условия равновесия грузов на Р. Архимед, основываясь на наглядном принципе симметрии и пользуясь понятием о центре тяжести; неизменяемая горизонтальная прямая, подпертая в своей середине останется в равновесии, если на ней будут привешены симметрично равные грузы на равных расстояниях. Приняв это, Архимед заменяет произвольное число таких грузов одним, равным сумме их и привешенным в их общем центре тяжести. Таким способом получается условие обратной пропорциональности грузов и расстояний, для соизмеримых отношений, посредством reductio ad absurdum (т. е. доказывая, что противное предположение ведет к невозможному заключению); условие это распространяется и на случай несоизмеримых отношений. Полное решение условий равновесия Р. дано было лишь Леонардо да Винчи, ясно сформулировавшего понятие о статическом моменте сил (см.). В настоящее время вопросы, касающиеся действия сил на Р., сводятся к частным случаям движения твердого тела около неподвижной оси. В курсах физики встречаются еще некоторые термины, связанные с понятием о Р.: «Р. первого рода» — у которого точка опоры расположена между точками приложения сил. «Р. второго рода» — когда обе точки приложения по одну сторону точки опоры. «Ломаный Р.» — у которого линия, соединяющая точку опоры с точками приложения, ломаная, а не прямая. «Чувствительный Р.» служит лишь для точных измерений и основан на том, что конец длинного плеча перемещается во столько раз больше конца короткого, во сколько он длиннее его. Такой Р. употребляется часовщиками для измерения диаметров проволоки и толщины листового металла; по форме он напоминает клещи для гвоздей, но один из длинных концов движется по разделенной дуге, прикрепленной к другому концу, и легкая пружина сдвигает короткие концы до прикосновения. Деления этой дуги не вполне равной длины, так как они должны быть пропорциональны хордам соответственных углов. Иногда конец одного Р. заставляют действовать на конец другого: такой Р. называют «сложным». В. Лермантов.
РЫЧАГ
м.Hebel m, Knüppel m; Kurbel fпродо́льный рыча́г баланси́рной подве́ски — Kurbelarm m, Längskurbel fрыча́г включе́ния стоя́ночного то́рмоза — Feststell. смотреть
Рычаг. Равновесие сил на рычаге
Содержание
С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).
В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
В обоих случаях у этого рычага есть неподвижная точка опоры – точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Таким образом, рычаги бывают двух видов (рисунок 3):
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Условие равновесия рычага
Рисунок 4. Рычаг.
Рисунок 5. Схематическое изображение рычага.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
С помощью таких опытов было установлено правило равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют – правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Примеры задач
Показать решение и ответ
Решение:
Запишем правило равновесия рычага:
$F_1 = F_2 \cdot \frac
СИ:
$0.1 \space кг$
$0.2 \space кг$
$0.5 \space м$
$0.2 \space м$
Показать решение и ответ
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 \frac<Н> <кг>\cdot (0.1 \space кг + 0.2 \space кг) = 9.8 \frac<Н> <кг>\cdot 0.3 \space кг \approx 3 \space Н$.
Запишем правило равновесия рычага:
Найдем массу груза:
$m_3 = \frac
Простые механизмы. Рычаг Архимеда.
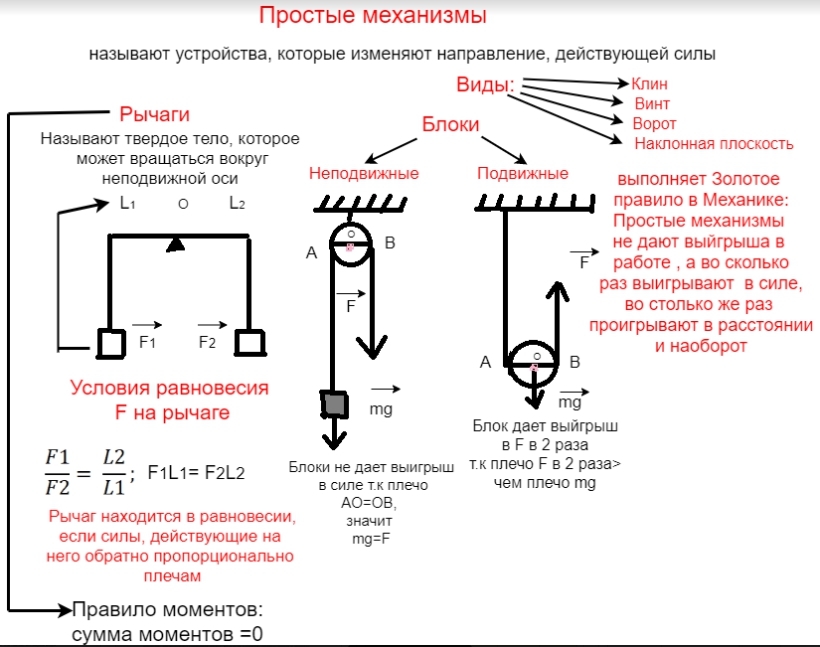
1. Понятие о простых механизмах
Называют устройства, которые изменяют направление действия силы.
2. История возникновения простых механизмов
Древнегреческий ученый Архимед первый создал и использовал простые механизмы, для защиты своего города Сиракузы от римлян.
3. Виды простых механизмов и их практическое значение
К простым механизмам относятся: наклонная плоскость, рычаг, блоки (подвижный и неподвижный), клин, винт, ворот. Примеры. Наклонная плоскость используется для подъема грузов на автомобили. Рычаг применяют в устройстве весов, подъемных кранов и т. д. Блоки применяют в устройстве лифтов. Клин удерживает колесо на оси автомобиля, велосипеда. Винт используют при изготовлении мебели. Ворот для подъема воды в колодцах.
4. Понятие рычага, его устройство и действие
Рычагом называют твёрдое тело, которое может вращаться вокруг неподвижной оси.
Рассмотрим устройства и действия рычага. У рычага есть ось вращения и плечи. Плечом называют кратчайшее расстояние от оси вращения до линии действия силы.
5. Условия равновесия сил на рычаге
Рычаг находится в равновесии, если силы действующие на него обратно пропорциональны плечам.
6. Формулы равновесия сил
М = F * L — момент сил, называют произведение силы на плечо.
Момент обозначается буквой М. Измеряется в единицах: Н * м.
7. Правила моментов
1. Рычаг находится в равновесии, если сумма моментов сил равна нулю.
2. Рычаг находится в равновесии, если сумма моментов сил вращающих рычаг по часовой стрелке, равна сумме моментов сил вращающих против часовой стрелки.
8. Блоки и получение выигрыша в силе и расстоянии
В механике используются блоки, которые бывают двух видов: подвижные и неподвижные. Неподвижный блок это колесо с желобом. Неподвижный блок используется для подъема различных грузов, но он не дает выигрыша в силе. Сила, приложенная для подъем, равна силе тяжести груза, так как плечо силы равно плечу груза. Подвижный блок дает выигрыш в силе в 2 раза, так как плечо силы в два раза больше плеча груза. Простые механизмы широко применяются в сельском хозяйстве, в быту, в технике и так далее.
9. Золотое правило механики
Для простых механизмов выполняется Золотое правило механики. Золотое правило заключается в том, что:
Простые механизмы не дают выигрыш в работе, во сколько раз выигрываем в силе, во столько же раз проигрывают в расстоянии и наоборот.