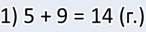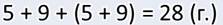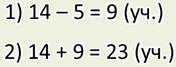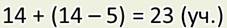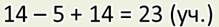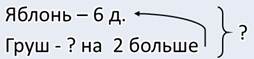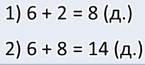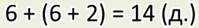Реши задачу по действиям и выражением что это

Реши задачу по действиям и выражением что это

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

Для ответа на вопрос задачи мы выполнили два действия.

Тогда количество всех рыб можно записать выражением:

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Различные способы решения задач и различные формы записи решения

Страницы работы

Содержание работы

На одном из уроков математики во II клас­се ученик, получив задание “Реши задачу”, спросил: “Каким способом нужно решать: по действиям или выражением”. Учитель ответил: “По действиям”.

Этот диалог показал, что и учитель, и уче­ник принимают различные формы запи­си решения за различные способы ее решения. Посещение уроков, беседы с учителями и учащимися позволили нам сде­лать вывод, что эта ошибка довольно распро­странена. Смешение же названных понятий приводит к тому, что, когда требуется дей­ствительно решить задачу разными способами, учащиеся либо вовсе не понимают задания, либо понимают его с большим трудом. А это, в свою очередь, снижает обучающие и воспитывающие возможности такого важного вида работы над задачей, как решение задач раз­ными способами.

Поэтому мы считаем своевременным обра­тить внимание учителей на отличие понятий способа решения задачи и формы записи решения задачи.

Задача считается решенной различными спо­собами, если се решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.

Рассмотрим, например, задачу № 522 из учебника математики для II класса: “Для уро­ков труда купили 4 катушки белых ниток, по 10 коп. за катушку, и 6 катушек черных ни­ток по такой же цене. Сколько денег уплатили за эти нитки?”

Эта задача может быть решена двумя ариф­метическими способами.

При первом из них, наиболее очевидном, первоначально определяют стоимость черных ниток: (10-4)-коп., затем стоимость белых ни­ток: (10-6) коп. и, наконец, стоимость всех ниток.

При втором способе замечаем, что цена 1 катушки белых ниток та же, что и черных, поэтому вначале можно узнать, сколько всего катушек ниток купили (6+4), а затем опре­делить стоимость всех этих ниток

Запись решения, для каждого способа может быть выполнена в нескольких формах. Пока­жем все эти формы для каждого способа ре­шения.

Запись решения по действиям с пла­ном.

1. Сколько стоят белые нитки? 10·4 = 40 (коп.)

2. Сколько стоят черные нитки? 10·6=60 (коп.)

3. Сколько денег уплатили за все эти нитки?

1. Сколько всего катушек с нитками купили?

2. Сколько денег уплатили за все эти нитки?

В настоящее время эта форма записи реше­ния задач в начальной школе практически не применяется. Однако мы считаем, что озна­комить с ней учащихся полезно и ее можно использовать на уроках математики, хотя и значительно реже, чем другие формы.

Рассмотрим другую форму записи решения той же задачи — это запись решения по дей­ствиям с пояснениями.

1. 10 · 4 =40 (коп) — стоимость белых ниток,

2. 10 ·6 = 60 (коп) — стоимость черных ни­ток.

3. 40+60=100 (коп.) — стоимость всех ни­ток.

1. 6+4 = 10 (шт.) — всего купили катушек ниток.

2. 10·10 = 100 (коп) — стоимость всех ниток.

Решение задачи можно также оформить по действиям без пояснений.

Ответ: все нитки стоят 1 руб.

Ответ: все нитки стоят 1 руб.

По задаче можно также составить выражение и найти его значение.

Ответ: все нитки стоят 1 руб

Ответ: все нитки стоят 1 руб.

Запись решения в этой форме осуществляется учащимися в два этапа. Вначале составляется выражение, затем учащиеся находят его значение, после чего запись решения приобретает вид равенства, в левой части кото­рого записано выражение, составленное по задаче, а в правой части — его значение.

Ни в коем случае нельзя называть запись 10 · 4 + 10 · 6 = 100 выражением, так как это противоречит тому определению поня­тия выражения, которое положено в основу изучения этого понятия в школе. Математи­ческое выражение составляется из цифр, букв, знаков арифметических действий и скобок, но не содержит знаков математических отноше­ний: равенства, неравенства и др. Два мате­матических выражения, соединенные знаком равенства, образуют равенство.

Приведенная выше запись — это равенство, левая часть которого есть выражение, составленное по задаче (10 · 4 + 10 ··6), а правая часть — выражение, состоящее всего лишь из одного числа (100), являющегося значением предыдущего выражения.

При проверке решения задачи, записанной в этой форме, учащимся можно дать такие задания:

1. Прочитайте выражение, составленное по задаче.

2. Назовите значение этого выражения. (Значение составленного по задаче выражения равно 100.)

3. Дайте ответ на вопрос задачи. (Все нитки стоят 100 коп., т. е. 1 руб.)

При решении задач следует правильно употреблять в своей речи соответствующие термины: Решите задачу и запишите решение по действиям с пояснениями. Решите задачу двумя способами, записав каждое решение в виде равенства, левая часть которого — выражение, составленное по задаче. Решите задачу двумя способами. Составьте соответствующие выражения и найдите их значения. Решите задачу и запишите решение вначале по действиям с пояснениями, а затем в виде выражения. Найдите значение этого выражения. Дайте ответ на вопрос задачи.

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

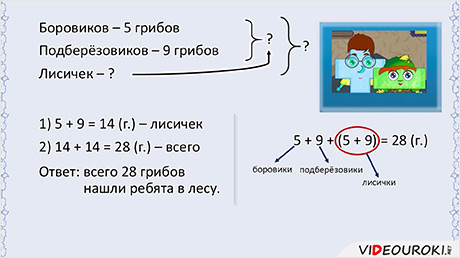
— Ну что же, приступим. Итак, вот первая задача:

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 22. Решение текстовых задач. Запись решения выражением

Перечень вопросов, рассматриваемых в теме:

— Что такое встречное движение, расстояние?

— Как выполнять схематический чертёж к задачам на движение?

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Теоретический материал для самостоятельного изучения

Расстояние – это путь, который прошёл какой-либо объект.

РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта

Измеряя расстояние, мы будем использовать сокращённые записи.

Сегодня на уроке мы будем решать новые задачи – задачи на движение.

Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?

Сделаем к задаче схематический чертёж.

Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.

Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.

Место встречи мальчиков будем обозначать флажком.

Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –

неизвестно. Поставим знак вопроса.

Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.

Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.

80 – 45 = 35 (м) прошёл второй мальчик.

Второй мальчик прошёл до встречи 35 метров.

Решим вторую задачу:

Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?

Сделаем схематический чертёж к задаче.

Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.

Будем решать задачу в два действия. Запишем первое действие:

1) 30 – 4 = 26 (м) прошла вторая девочка.

Вторая девочка прошла до встречи двадцать шесть метров.

Теперь можем ответить на вопрос задачи. Запишем второе действие:

2) 30 + 26 = 56 (м) длина дорожки.

Длина всей дорожки была 56 метров.

Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.

1.Подберите схематический чертёж к задаче

Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?

2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.

30 – 20

30 + 20

70 – 45

70 – 45

30 + 20

30 – 20

Источник

Конспект урока по математике на тему «Решение задач по действиям и с помощью выражения» (3 класс)

МБОУ Зимовниковская средняя общеобразовательная школа №10

по математике в 3 «Б» классе

учитель начальных классов

Тема: Решение задач по действиям и с помощью выражения.

Цель : формировать умение записывать решение задач в виде выражения и по действиям; продолжить формирование навыка выполнения действий в выражениях со скобками и без скобок.

закрепить решение задач по действиям и выражением;

закреплять знание таблицы умножения и деления;

развивать познавательную активность, внимание, память обучающихся;

воспитывать интерес к математике;

воспитывать толерантное отношение друг к другу, взаимное сотрудничество.

Тип урока: урок – закрепление.

Формы организации учебной деятельности: индивидуальная, фронтальная, парная, групповая.

Методы: проблемный, частично-поисковый, фронтальная беседа, словесный, наглядный.

Технологии : здоровье сберегающие, личностно-ориентированные, развивающие.

Формируем умение слушать и понимать других.

Формируем умение строить речевое высказывание в соответствии с поставленными задачами.

Формируем и отрабатываем умение согласованно работать в группах и коллективе.

Формируем умение извлекать информацию из текста и иллюстрации.

Формируем умение высказывать своё предположение на основе работы материала учебника.

Формируем умение составлять план деятельности на уроке с помощью учителя.

Формируем эмоциональное отношение к школе и учебной деятельности.

Формируем общее представление о здоровом образе жизни.

— компьютерная презентация, карточки с алгоритмом самооценки, карточки для групповой работы.

Мотивация к учебной деятельности.

Работа в рабочей тетради

Работа в рабочей тетради

Формулирование темы урока.

Постановка цели урока.

Постановка задач урока.

Закрепление изученного материала.

Подведение итога урока.

Поприветствуйте, ребята, гостей,

Улыбнитесь друг другу веселей

Я желаю всем успехов и добра,

А теперь урок начать пора

Задание 1 ряду, 2 ряду, 3 ряду

Оцените свою работу(«+», «-»)

Запишите число, классная работа.

1 обучающийся у доски.

Записать одни ответы.

5 увеличить в 2 раза

15 уменьшить в 3 раза

Во сколько раз 16 больше 4

Во сколько раз 3 меньше 9

На сколько 10 больше 5

Обучающийся называет ответы на доске, класс проверяет.

Оцените свою работу(«+», «-»)

А какие продукты видите на слайде

Какая возникла проблема?

Все ли продукты полезны?

Правильные продукты выбрала Катя?

Как называется такое питание?

О чём мы будем говорить на уроке?

Запишите задачу по действиям, а 3 обучающихся записывают выражением.

Что можете сказать вредно или полезно употреблять эти продукты в пищу?

Мы говорили о питании. (прикрепим лучик)

Что мы сейчас решали?

Сформулируйте цель урока, т.е. чему будем учиться на уроке?

Сформулируйте задачи урока:

Какие средства помогут нам открыть новые знания на уроке? Кто и что нам помогает? Откуда вы сможете получить эту информацию?

У вас на парте условие задачи.

О чём говорится в задаче?

Записать решение по действиям, а 2 пары выражением (проверка)

Прикрепляем лучик спортивные секции

Гимнастика для глаз, спортивные движения

Чтение задачи про себя.

С какими сложными словами встретились?

Российский гребец Роман Аношкин –

Бронзовый призёр Олимпиады – 2016 года в Рио-де-Жанейро на дистанции 1000 метров а байдарке.

Прикрепляю лучик «Спорт»

распределились по группам.

— Вспомним правила работы в группе.

Получите жетоны и займите место в своей команде.

Решить задачу и ответить на вопрос.

Учебник с.101 Задача №308

составить математический диктант.

Какие задачи ставили?

Удалось ли решить поставленные задачи? Каким способом?

Какие получили результаты?

Где можно применить новое знание, умение?

Что на уроке у вас хорошо получилось? Над чем ещё надо поработать?

Ребята, вы прекрасно работали на уроке, молодцы. Спасибо вам за урок.

У каждого ученика лист самооценки

8 – это однозначное число, чётное, предыдущее число 7, последующее 9

Чипсы, колу булочку, кириешки, сок, жевательную резинку «Дирол»

О здоровом образе жизни.

1)20+10=30( руб.) – стоит покупка.

2)200-30=170 (руб.)- сдача.

По действиям и выражение

Решение задач по действиям и выражением.

научиться решать задачи, сравнивать числовые выражения.

применять новые знания на практике;

закреплять знание таблицы умножения и деления;

Учебник, учитель, наш жизненный опыт, общение друг с другом.

О спортивных секциях

1)3*3=9(уч.)-посещают секцию волейбола.

2)21-9=12(уч.)-посещают другие секции.

1)5*7=35 (ч.)- в 7 командах по гребле.

2)9*6=54(ч.)- в 6 командах в стрельбе.

Ответ: на 19 человек больше участвовало в стрельбе.

Работать дружно, говорить по одному; уметь слышать друг друга.

Выступление командиров групп.

Дети раздают жетоны и рассаживаются по местам.

закреплять знание таблицы умножения и деления;

На доске незаконченные предложения.

« Я похвалил бы себя за …»

Мне было интересно…

Личностные УУД:
выражать положительное отношение к процессу познания, проявлять желание к новому познанию.

нацеливание на успешную деятельность.

Коммуникативные УУД: формулирование умения слушать и слышать, аргументировать своё мнение.

осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Познавательные УУД: Ориентироваться на разнообразие способов решения заданий

Самостоятельно объяснять информацию; понимать, объяснять и осознанно воспроизводить учебные алгоритмы.

Личностные УУД: учебно-познавательный интерес к новому учебному материалу и способам решения задачи.

принимать участие в обсуждении и формулировании темы и целей урока.

Регулятивные УУД : принимать и сохранять учебную задачу.

Познавательные УУД: осуществлять анализ объектов с выделением существенных и несущественных признаков.

Регулятивные УУД: принимать и сохранять учебную задачу.

Познавательные УУД: осуществлять поиск необходимой информации.

Регулятивные УУД: принимать участие в обсуждении и формулировании целей конкретного задания.

Личностные УУД: учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи.

Личностные УУД: Ориентация на понимание причин успеха в учебной деятельности, в том числе на самоанализ и самоконтроль результата.

Коммуникативные УУД: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.

Способность к самооценке на основе критериев успешности учебной деятельности.

Познавательные УУД: Проводить сравнение и классификацию по заданным критериям.

Коммуникативные УУД: Формулировать собственное мнение и позицию.

Коммуникативные УУД: Допускать возможность осуществлять у детей различных точек зрения.

Математика. 3 класс. Учебник для 3 класса общеобразовательных учреждений в 2 частях. Часть 1/ Н.Б. Истомина – 10-е изд. перераб. и доп. – Смоленск: Ассоциация XXI век, 2012г.

2.Математика. 1-4 классы: Упражнения для устного счёта/ Сост. М. В. Голович, Ю. К. Бондаренко и др. Волгоград: Учитель, 2015.

3.Математика. 3 класс. Методические рекомендации/ Н.Б. Истомина-16-е – 4-е изд. Смоленск: Ассоциация XXI век, 201 5 г.

Задания для индивидуальной работы (по рядам).

Я называю число вы к каждому последующему числу прибавьте 6 и если число будет чётное вы поднимите руку. Число 4.

Я называю число вы каждое последующее число увеличьте на 5 и если это число делится на 2 вы хлопаете в ладоши. Число 5.

Задание для парной работы.

В нашем классе 21 ученик. 3 ученика посещают секцию футбола, а секцию волейбола посещают в 3 раза больше учеников. Сколько учеников нашего класса посещают другие секции?

Задания для групповой работы.

Коля соблюдал режим дня и делал зарядку, Петя забывал делать зарядку.

Коля сделал 18акробатических упражнений, а Петя 9 акробатических

упражнений. Во сколько раз больше сделал упражнений Коля, чем Петя?

Вопрос: Почему Петя сделал упражнений меньше, чем Коля? ( устно)

Игорь регулярно посещал секцию по плаванию, а Сергей прогуливал тренировки.

Ребята плавали в бассейне. Игорь проплыл 8 метров, а Сергей в 2 раза меньше. Сколько метров проплыл Сергей?

Вопрос: Почему Сергей проиграл в состязании по плаванию? (устно)

Фёдор и Андрей состязались в беге на лыжах. Андрей ведёт здоровый образ жизни, а Фёдор ведёт малоподвижный образ жизни, мало бывает на свежем воздухе.

Фёдор прошёл дистанцию 5 км, а Андрей в 3 раза больше. Дистанцию какой длины прошёл Андрей?

Вопрос: Почему Фёдор проиграл в состязании в беге на лыжах? (устно)

Оля и Ира на свежем воздухе прыгали на скакалке. Ира любила очень много кушать пирожных.

Оля прыгнула 20 раз, а Ира 10 раз. Во сколько раз меньше прыгнула Ира, чем Оля?

Вопрос: Почему Ира прыгнула на скакалке меньше, чем Оля.(устно)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-187361

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Рособрнадзор объявил сроки и формат ЕГЭ

Время чтения: 1 минута

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник