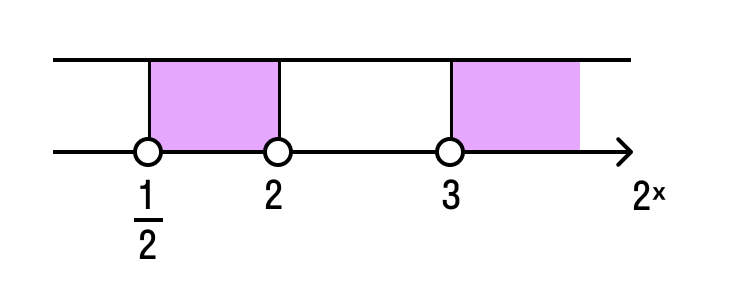
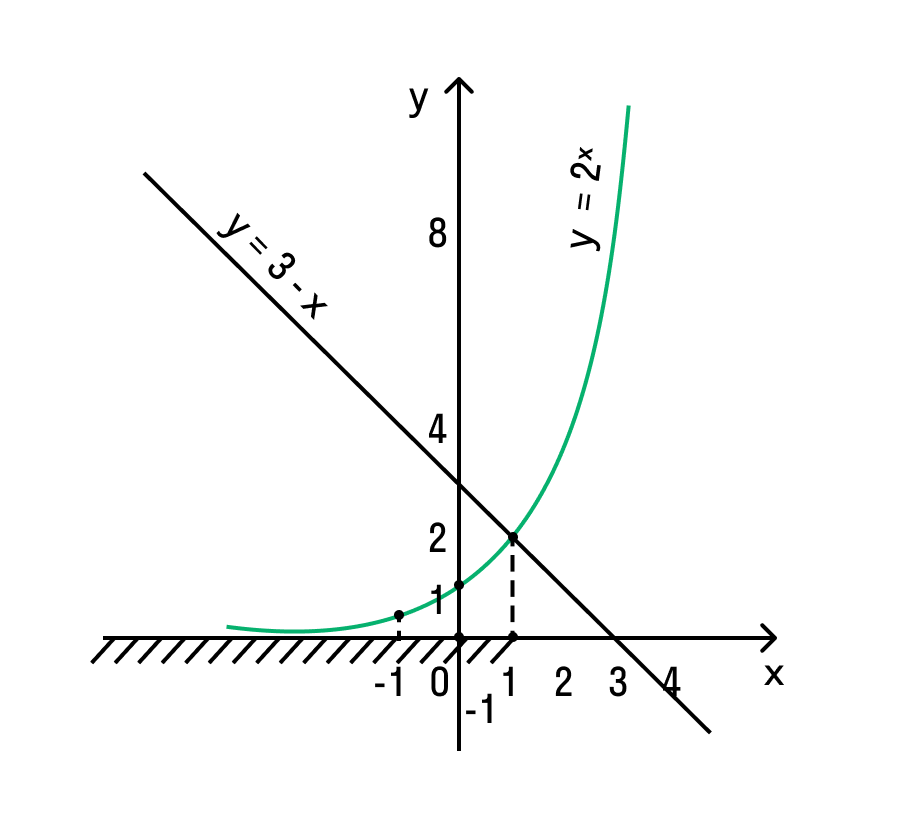
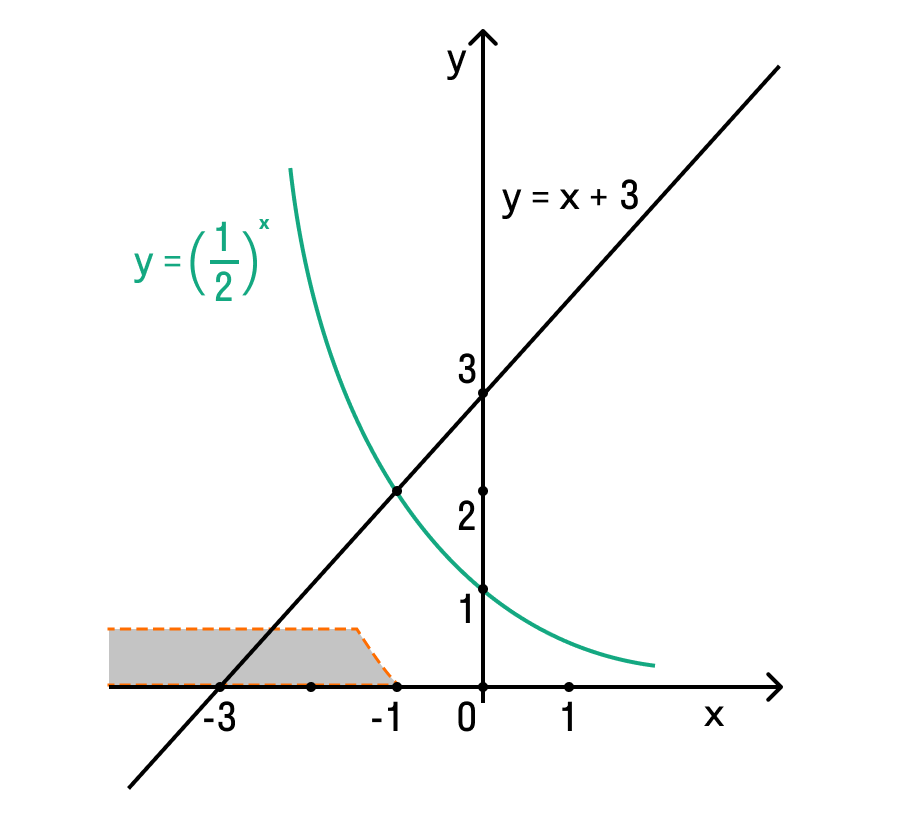
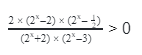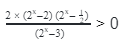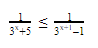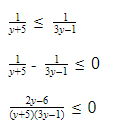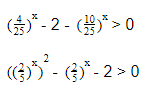Реши неравенства что в них интересного
Урок-проект по математике на тему «Неравенства»


Творческое название: «Путешествие в страну неравенств»
Математика как наука обладает уникальным эффектом. Она по высказыванию М.В. Ломоносова «Ум в порядок приводит». В 3 –ем классе продолжается формирование у учащихся важнейших математических понятий, связанных с числами, величинами, отношениями, элементами алгебры и геометрии.
Данный проект подводит итог работы с неравенствами, рекомендует способы решения неравенств, применение их в жизненных ситуациях и подготавливает к более сложному материалу «Координатный луч», составление и решение неравенств по координатному лучу.
Зачем мы учимся решать неравенства?
Проблемные вопросы учебной темы:
Что такое неравенство, виды неравенств.
Способы решения неравенств.
Решение задач с использованием неравенств.
Темы исследований учащихся:
Когда появились неравенства?
Как решить неравенства?
Где в жизни я могу использовать неравенства?
Дидактические и организационные материалы;
*Развивать познавательный интерес к математике.
*Стимулировать творческую активность учащихся в процессе добывания новых
*Использовать полученные знания в своей повседневной жизни.
*Формировать навыки работы в группах.
*Воспитывать любовь к математике, развивать логику мышления
*Привлекать родителей к участию в процессе осуществления проектной
* Закрепить знания решения неравенств различными способами.
*Учить кратко излагать свои мысли, доказывать.
Материалы и оборудование: компьютер, тесты, весы.
Формы представления результатов исследования и критерии их оценивания:
Этапы работы над проектом
Этап 1. Разработка проектного задания:
-тема исследований учащихся;
-выбор критериев оценки результатов.
Класс делится на 3 группы, которые получают задания.
Группа 1 «Исследователи» — собрать теоретический материал о неравенствах;
-доказать, что в природе существуют неравенства;
Тема исследования : «Когда появились неравенства?»
Группа 2 «Теоретики» — решить неравенства различными способами;
— кратко изложить свои мысли;
Тема исследования: «Как решить неравенства?»
использовать неравенства?» (мини – сочинения);
-оформить математический бюлетень «Думай, считай,
Этап 2. Разработка проекта:
Задачи этапа –сбор и уточнения информации.
-у ченики самостоятельно работают по группам;
— распределяют между собой задания;
-анализируют собранный материал;
— учитель наблюдает, помогает.
Этап 3. Оценка, результат:
Задачи этапа – анализ выполненных заданий;
-ученики готовятся к представлению материала на уроке –
Этап 4. Защита проекта:
одноклассниками, родителями, учителями.
Учитель: — Ребята, наше занятие Клуба знатоков математики сегодня
будет не совсем обычным.
Сегодня у нас присутствуют гости, давайте поприветствуем их.
На занятии нам предстоит очень интересная исследовательская работа.
— Скажите, какими качествами нужно обладать ученику, чтобы он
сделал для себя открытие? (Нужно быть внимательным, наблюдательным,
активным, уметь поддерживать товарища)
-Перед вами «Дерево решений» (на магнитной доске)
Вы знаете это волшебное дерево. На нём могут созреть любые плоды,
а может, не вырасти ничего. Всё зависит от вас, от того, как вы
— Давайте же все будем внимательными, точными и активными, чтобы
достичь цели в исследовательской работе и на ДЕРЕВЕ выросли плоды
— Итак, все настроились на работу, проверили посадку, открыли
исследовательские журналы, записали число. (6 ноября )
— Сегодня у числа 6 День рожденья. Исследуйте его.
(Оно однозначное, состоит из 6 единиц, число 6
делится на 1, 2, 3 и 6, оно меньше 7, но больше 5)
-Итак, ребята, тема нашего занятия «Путешествие в страну Неравенств».
Мы уже встречались с ними на уроках математики, умеем решать пока
простые виды неравенств, но «Ч тобы математику понять
И постичь неведомые таинства,
Кроме уравнений и неравенства .
— И перед нами будут стоять сегодня следующие вопросы:
Когда появились неравенства?
Что такое неравенство?
Как решать неравенства?
Что значит решить неравенство?
Где в жизни можно использовать нер-ва?
-Ответы на них мы должны дать в ходе нашего занятия.
-Исследуя тему «Неравенства», мы распределили эти проблемные вопросы по
группам и назвали их так:
Исследователи , где ребята «копали» историю неравенств.
Теоретики исследовали, как решать неравенства .
Практики доказывали, Как и Где можно использовать неравенства.
Народная мудрость гласит: «Скажи мне, и я забуду.
Позволь мне это сделать самому,
и это станет моим навсегда».
Под таким девизом работали группы, исследуя свои вопросы.
Итак, приступаем к работе. Вспомним правила работы в группе. ( НАЗЫВАЮТ)
Слово предоставляется нашим исследователям:
Ученик-исследователь 1: Мы с ребятами искали ответ на вопрос «Когда появились неравенства?» В ходе исследования узнали много нового и интересного и, используя полученные знания по теме «Неравенства», выпустили математический бюллетень.
Бюллетень о неравенствах:
Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки в III в. до н. э.
Ученик исследователь 1 : У неравенств такие же свойства как и у равенств. Неравенства возникли после того, как в результате работ немецкого математика ГАУССА и русского математика П. Л. Чебышева, была поднята роль приближенных значений.
В настоящее время всюду, где рассматриваются задачи с приближенными решениями, появляются неравенства.
Ученик-исследователь 3: Неравенства бывают числовыми, например: 48 : 6 , с одной или несколькими переменными а + в > c .
Неравенство может быть верным 5*3 > 5*2 или неверным 5*3 Решая или доказывая неравенства, мы опираемся на основные свойства отношения «больше или меньше» между числами.
Учитель : Наши Исследователи еще хотят показать КАК ПРИШЛИ В НАШУ
ЖИЗНЬ НЕРАВЕНСТВА и ЧТО неравенства в жизни существуют
всюду. Давайте послушаем их.
Я бы хотел доказать, что неравенства существуют в нашей жизни и очень часто. Свой эксперимент я покажу на весах. (СНАЧАЛО НА ЧИСЛОВЫХ)
Еще в 1 классе, изучая числа, мы учились сравнивать их. Представляли
число в количестве и даже сравнивали его на вес. Например: сравним число 9 и 7. (ВЗВЕШИВАЕМ) Что мы видим? 9 > 7, а 7
А сейчас я покажу другой жксперимент.
На одну чашку весов я положу пряник, а на вторую – конфету.
Что мы видим? Чашка с пряником перевешивает чашку с конфетой.
Вес неравный. Делаем вывод : пряник тяжелее конфеты.
— А сейчас, ребята, расскажут о своих наблюдениях .
Наблюдая в жизни, изучая неравенства я пришел к выводу, что неравенством можно показать вес грузовой машины и легкового автомобиля. а > в или в
Ученик- исследователь 6:
А я хочу показать неравенством кто выше : утенок или котенок. Их также можно сравнить неравенством и по весу: с d d > с
Ученик –исследователь 7 : Исследуя тему «Неравенства», я решила, а почему бы не сравнить наш дом и дом бабушки по высоте и площади, показать это неравенством: x > y или y x .
Учитель: Спасибо, исследователям . Вы хорошо исследовали и доказали, что неравенства в нашей жизни существуют, их можно видеть всюду, а мы на уроках математики будем учиться их решать.
— А сейчас, мы проведем математическую разминку, где покажем, как мы уже умеем решать неравенства.
Разминка – тесты (устно)
1. Найдите неравенства: (т. к. нер-ва это сравнение чисел и величин
с помощью знаков больше или меньше)
б) а + в > c г) а + в = с + а верно (б, в)
2. Поставь знак, чтобы получилось верное неравенство:
3. Подбери и вставь числа, чтобы получились верные неравенства :
а) 5 * 3 5 * 7 верно (в)
Учитель: Молодцы, ребята! А теперь слово даем ТЕОРЕТИКАМ. Они покажут способы решения неравенств.
Ученик-теоретик 1: Перед нами стоял проблемный вопрос «Как решить неравенство?» Мы долго думали, решали, спорили и пришли к выводу, что неравенство можно решить разными способами.
Я докажу решение неравенства Х – 37 путем подбора. Неравенство будет верным, если вместо переменной Х подставлю числа, которые в значении разности дадут число меньше 29.
Подбираю числа. Начинаю с 38, т. к. 38 больше 37 и разность равна 1, а 1 Дальше исследую другие числа больше 38. К примеру, число 47. 47 минус 37 равно 10, а 10 меньше 29. Неравенство верно. Проверю числом 70.
65 – 37 Делаю вывод , что решением неравенства будут числа от 38 до 65.
Ученик-теоретик 2 : А я хочу доказать решение неравенства с помощью
Итак, дано неравенство У – 15 > 30 . Сначала узнаю, при каком значении неизвестного получится равенство. Для этого составляю уравнение У–15 = 30 . Решаю его.
Нам неизвестно уменьшаемое. Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое : У= 30+15. Считаю правую часть У = 45 . Проверяю:
45 – 15 = 30. 30 = 30 . Следовательно, корень уравнения равен 45.
Возвращаемся к неравенству. Подставляем в неравенстве число 45. Получаем: 45 – 15 = 30 . Следовательно, надо увеличить уменьшаемое, чтобы разность стала больше, чем 30. Значит, решениями неравенства будут числа больше 45. Проверяю:
Тоже верно, потому что 85 больше 30.
Учитель : Молодцы, ребята, умело доказали способы решения неравенства.
-А теперь, пришло время отдохнуть.
Командир группы теоретиков: Мы предлагаем для закрепления решить неравенства тем способом, который удобен и понятен вам.
(На доску вывешиваются 2 неравенства)
Работа в журналах : / у доски 2 уч-ся одновременно/
1 . Решить неравенство (путем подбора)
а) Х : 7 Х= 35, 28, 21, 14, 7, 0
( в правой части большее число, чем в левой. В левой будет меньше 6, это 35:7=5, 28:7=4,
При Х равном 35, 28, 21, 14, 7, это неравенство будет верным.
2. Решить неравенство с помощью уравнения.
х > 2 x = 2 (неизвестное число – второй множитель,
он равен 2, значит в нерав-ве множитель
надо увеличить, взять 3 …. 10 и т.д
Гимнастика для глаз : нарисовали глазами овал, а теперь нарисуйте овал
по-больше; А сейчас нарисуйте квадрат и впишите
в него треугольник.
— Молодцы, ребята, глазки отдохнули и опять за работу.
Учитель : Нашим практикам достался серьезный вопрос. Они выясняли, где
в жизни могут использоваться неравенства. Давайте послушаем их.
(РЕШЕНИЕ ЗАДАЧИ с помощью нер-ва 2-мя способами)
Ученик – Практик 1 : К примеру, на праздник «Золотая осень» мы собираем
композиции из цветов. В букете было 43 дубочка. Когда
мы взяли из букета несколько цветов, то в нем осталось больше 15.
Сколько же цветов мы могли взять, чтобы составить другую композицию?
На доске дается краткая запись задачи: БЫЛО – 43
Следовательно, мы могли взять от 1 до 27 цветочка для составления композиции.
Ученик – практик 2: (дается краткая запись задачи, ребята по ней составляют условие к задаче и решают с помощью уравнения)
На школьном дворе мы с ребятами собирали каштаны. Для своей поделки использовали 14 каштанов и у нас осталось меньше 14. Сколько всего каштанов мы собрали?
У – 14 Учитель: Молодцы, ребята! Вы теперь знаете, что и задачу можно решать
с помощью неравенства, т. е. неравенства в жизни можно
1 . Когда появились неравенства? (Неравенства появились очень давно . Нерав- ва в математике первыми доказали математики Гаусс и Чебышев)
2. Так что же такое НЕРАВЕНСТВО? (Нерав-во – это сравнение чисел величин с помощью знаков больше и меньше)
3. Как решаются неравенства? (Нер-ва решаются путем подбора и с помощью
4. Что значит решить неравенство? (…значит найти все значения Х, которые
подходят данному неравенству)
5. Где в жизни можно использовать неравенства? ( При сравнении любых предметов, в решении задач, даже можем узнать насколько больше или меньше одно число от другог
6. Приведите примеры из жизни с использованием неравенств. (По росту уч-ся, по весу портфелей, размер классной доски, размеры ученического стола и учительского, рост учителя и ученика и т. д.)
Учитель: Верно, ребята. Неравенства в жизни всюду и мы вместе доказали это.
Посмотрите на это неравенство: х * 7 + 45 : 9 > 75 – ( 20 : 4) . Сложно? Интересно? Совсем скоро вы научитесь решать и такие неравенства!
А сейчас скажите, кто был сегодня на уроке внимательным, активным и точным?
Какая группа провела серьезную работу в исследовании неравенств? (Ученики обмениваются мнениями: Что получилось?
Рефлексия: Над чем надо поработать?)
(активные участники награждаются символическим Солнышком со
Реши неравенства что в них интересного
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
Неравенством называют высказывание, в записи которого используют знаки > или 2, а > 7, x 0 верно, а неравенство 3 > 5 неверно, так как 3 меньше 5.
Неравенство y 8. Иначе говорят, что число 3 удовлетворяет данному неравенству, а число 20 не удовлетворяет.
Исходя из этого, можем сделать вывод, что решение неравенства – это значение переменной, которое при подстановке в неравенство превращает его в верное высказывание. Решить неравенство означает найти все решения данного неравенства.
Так, число 3 является решением неравенства y § 2 Множество решений
Множество решений неравенства – это полный список решений этого неравенства.
Неравенство y+ 6 4. Множество решений этого неравенства является пустым множеством: Ø.
Рассмотрим еще два неравенства: b 5.
Стоит отметить, что решения неравенства на числовом луче изображаются закрашенными кружками, а граница неравенства (число 5) не закрашенным кружком, так как данное неравенство является строгим.
Решим неравенство b § 3 Краткие итоги по теме урока
1. Решение неравенства – это значение переменной, которое при подстановке в неравенство превращает его в верное высказывание.
2. Решить неравенство означает найти все решения данного неравенства.
3. Множество решений неравенства – это полный список решений неравенства.
Показательные неравенства
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательных неравенств
Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.
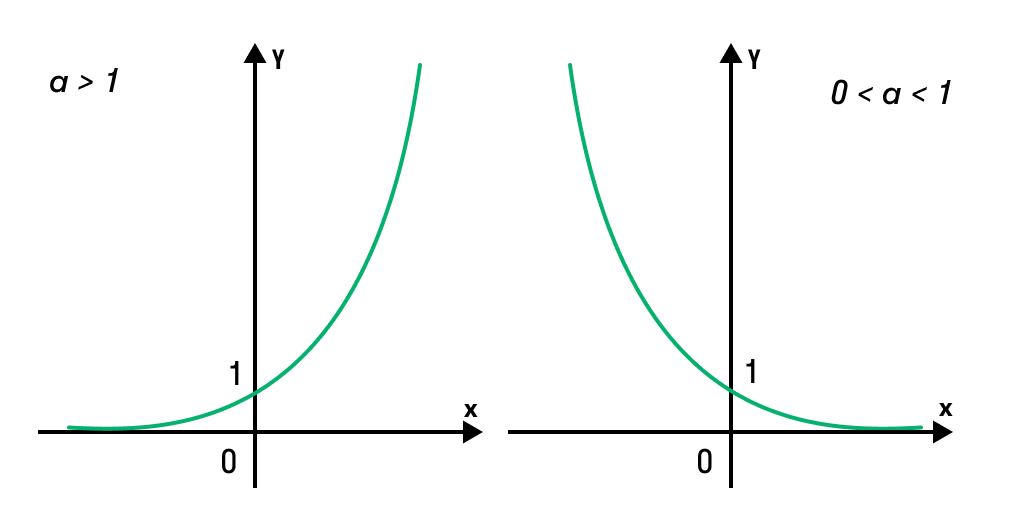
Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.
Допустим, у нас есть простейшее показательное неравенство:
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
Проверим, верно ли в таком случае х > 2.
Как видите, на самом деле в этом случае х