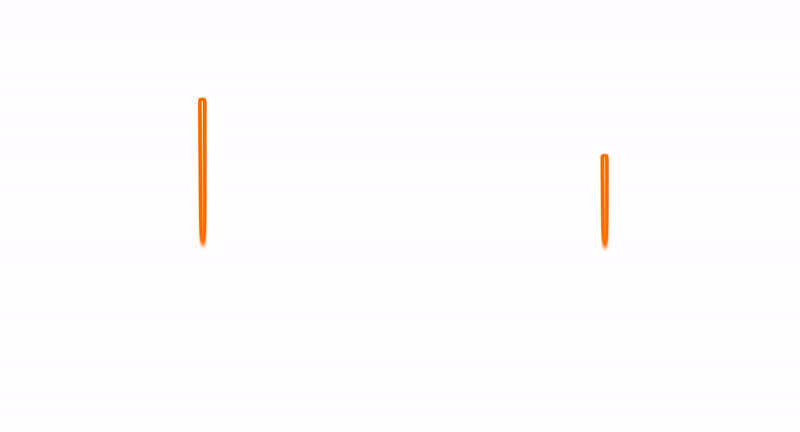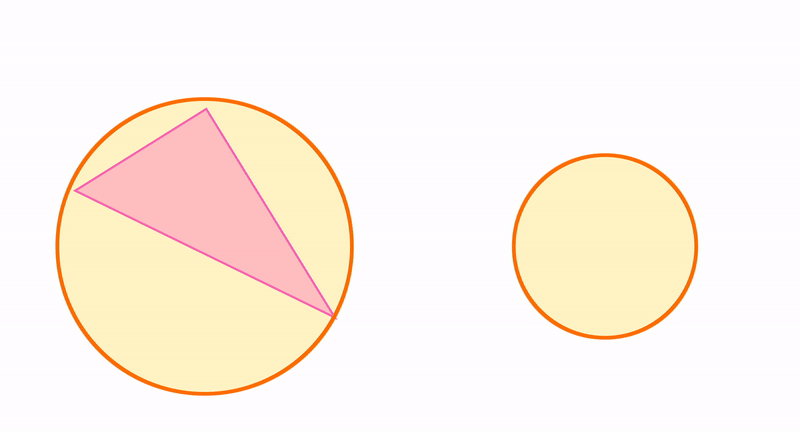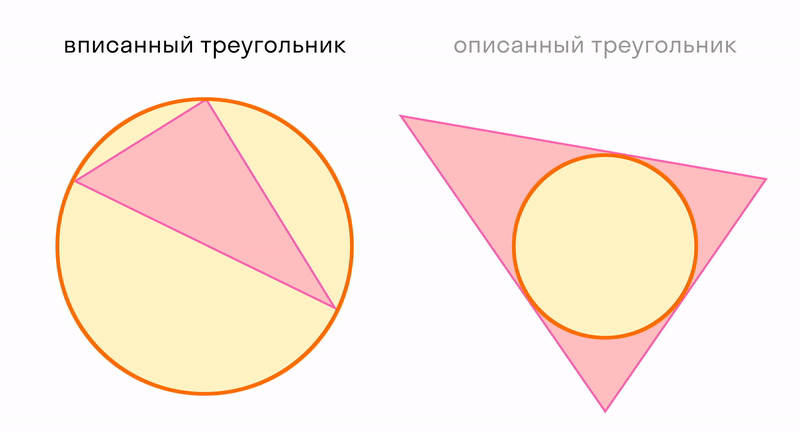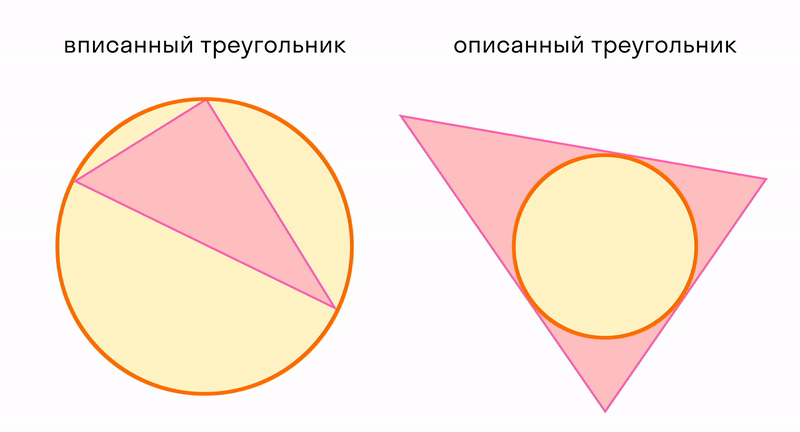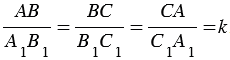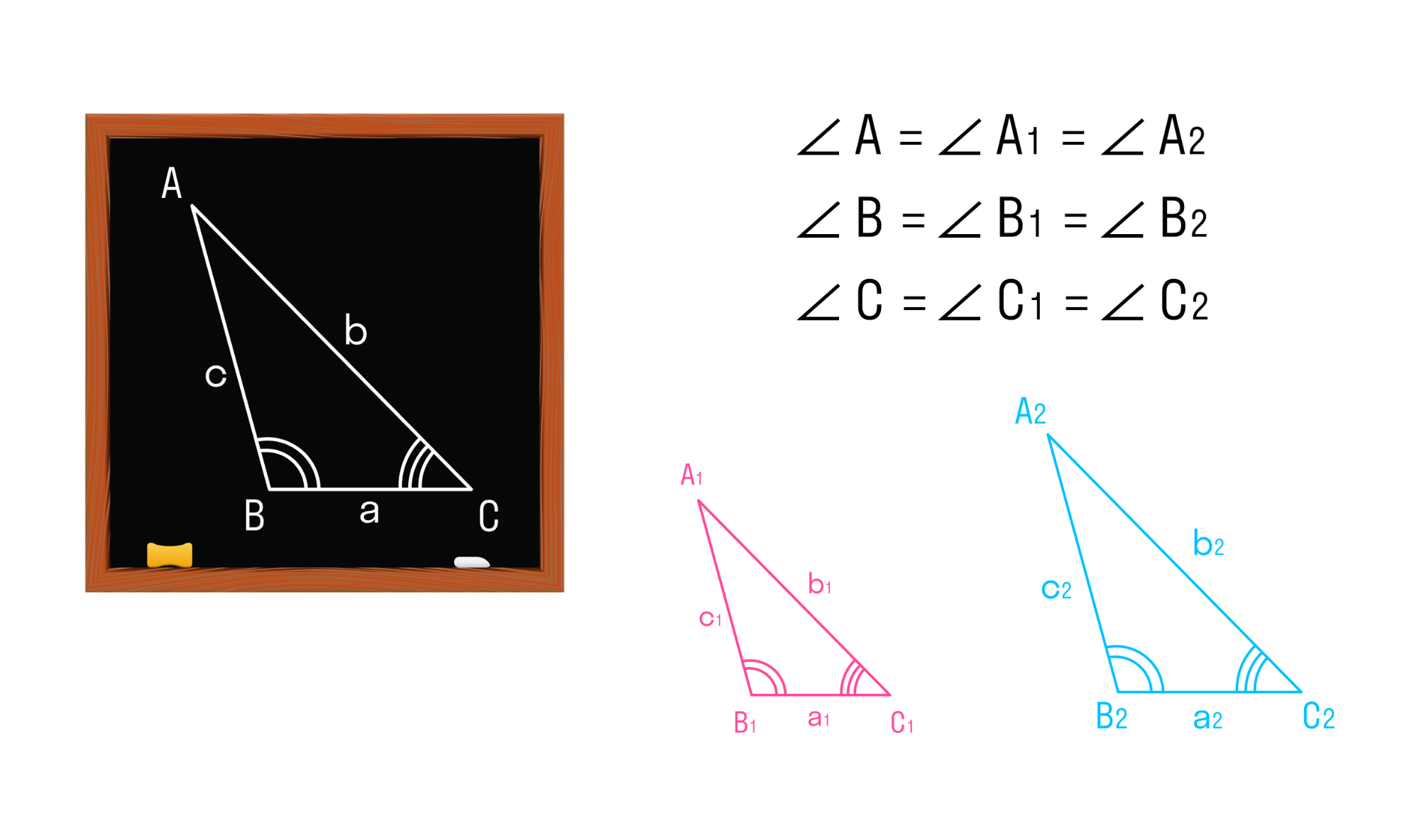С чего начинается геометрия в 8 классе

С чего начинается геометрия в 8 классе

Геометрия 8 Атанасян Поурочные планы. Подробное поурочное планирование по геометрии для 8 класса (УМК Атанасян и др.), ознакомительная версия. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». При постоянном использовании необходимо купить книгу: Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: Просвещение. Цитаты из пособия использованы в учебных целях.

Геометрия 8 класс. УМК Атанасян.
Поурочные планы

Вводное повторение

Урок 1. Вводное повторение.
Урок 2. Вводное повторение

ГЛАВА V. ЧЕТЫРЕХУГОЛЬНИКИ

Урок 3. Многоугольники.
Урок 4. Решение задач по теме «Многоугольники».
+ Самостоятельная работа № 1 «Многоугольники».
Урок 5. Параллелограмм.
Урок 6. Признаки параллелограмма.
Урок 7. Решение задач по теме «Параллелограмм».
+ Самостоятельная работа № 2 «Параллелограмм».
Урок 8. Трапеция.
Урок 9. Теорема Фалеса.
Урок 10. Решение задач на построение.
Урок 11. Прямоугольник.
Урок 12. Ромб. Квадрат.
Урок 13. Решение задач по теме «Прямоугольник. Ромб. Квадрат».
Урок 14. Осевая и центральная симметрии.
Урок 15. Решение задач. Подготовка к контрольной работе.
Урок 16. Контрольная работа № 1 по теме «Четырехугольники».

ГЛАВА VI. ПЛОЩАДЬ

Урок 17. Площадь многоугольника.
Урок 18. Площадь прямоугольника.
Урок 19. Площадь параллелограмма.
Урок 20. Площадь треугольника.
Урок 21. Площадь треугольника.
Урок 22. Площадь трапеции.
Урок 23. Решение задач на вычисление площади.
Урок 24. Решение задач на вычисление площади.
Урок 25. Теорема Пифагора.
Урок 26. Теорема, обратная теореме Пифагора.
Урок 27. Решение задач по теме «Теорема Пифагора».
Урок 28. Решение задач. Подготовка к контрольной работе.
Урок 29. Решение задач. Подготовка к контрольной работе.
Урок 30. Контрольная работа N° 2 по теме «Площадь».

ГЛАВА VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

ГЛАВА VIII. ОКРУЖНОСТЬ

Урок 51. Взаимное расположение прямой и окружности.
Урок 52. Касательная к окружности.
Урок 53. Решение задач по теме «Касательная к окружности».
Урок 54. Градусная мера дуги окружности.
Урок 55. Теорема о вписанном угле.
Урок 56. Теорема об отрезках пересекающихся хорд.
Урок 57. Решение задач по теме «Центральные и вписанные углы».
Урок 58. Свойство биссектрисы угла.
Урок 59. Серединный перпендикуляр.
Урок 60. Теорема о точке пересечения высот треугольника.
Урок 61. Вписанная окружность.
Урок 62. Свойство описанного четырехугольника.
Урок 63. Описанная окружность.
Урок 64. Свойство вписанного четырехугольника.
Урок 65. Решение задач. Подготовка к контрольной работе.
Урок 66. Контрольная работа № 5 по теме «Окружность».

Повторение

Урок 67. Повторение по темам «Четырехугольники», «Площадь».
Урок 68. Повторение по темам «Подобные треугольники», «Окружность».
Урок 69. Контрольная работа № 6 (итоговая).
Урок 70. Учебно-исследовательская конференция.

Подробные поурочные разработки, методические советы и рекомендации, тексты самостоятельных и контрольных работ, тестовые задания, дополнительные задачи по каждой теме, задачи повышенной сложности. Практически все задачи, проверочные работы сопровождаются указаниями для обучающихся, ответами и краткими или подробными решениями для экономии времени учителя при подготовке к уроку, для эффективной работы над ошибками, организации дифференцированной работы.

Уроки включают различные виды деятельности обучающихся: практическую работу, работу в парах и группах, самостоятельную работу с использованием различных форм проверки.

Планирование предусматривает достижение не только предметных результатов, но и личностных (формирование представлений о математике как о части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества; развитие логического и критического мышления, умения работать в группе, команде; уважение мнения товарищей) и метапредметных (умения анализировать и осмысливать текст задачи, извлекать из текста необходимую информацию, моделировать с помощью схем, рисунков, реальных предметов, строить логическую цепочку, оценивать полученный результат, осуществлять самоконтроль, доказывать и опровергать утверждения с помощью контрпримеров, классифицировать, исследовать простейшие закономерности).

Пособие будет полезно в первую очередь начинающему учителю, который сможет позаимствовать полностью предлагаемые сценарии уроков, а также опытному педагогу для использования их частично, встраивая в собственный план урока.

Геометрия 8 Атанасян Поурочные планы. Подробное поурочное планирование по геометрии для 8 класса (УМК Атанасян и др.), ознакомительная версия. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Источник

С чего начинается геометрия в 8 классе

Геометрия — математическая наука о пространственных формах, размерах и соотношениях геометрических объектов (фигур, тел). Слово «гeoметрия» греческого происхождения («geo» — земля, «metreo» — измеряю).

Планиметрия — раздел геометрии,в котором изучают свойства фигур,расположенных в одной плоскости. Слово «планиметрия» происходит от латинского корня «planum» — плоская поверхность и греческого — «metreo» — измеряю.

Стереометрия — раздел геометрии, в котором изучают свойства пространственных тел. Слово «стереометрия» происходит от греческих слов «stereos» — пространственный, «metreo» — измеряю.

Периоды развития геометрии

I период — зарождение геометрии как математической науки, начало которого теряется в глубине столетий, а концом считают V в. до н.э. Этот период характеризуется накоплением фактов и установлением первых зависимостей между геометрическими фигурами. Начался он в Древнем Египте и Вавилоне, в VII в. до н.э. Эти знания были перенесены в Грецию, где постепенно они начали оформляться в четкую систему.

II период — (V в. до н.э. — XVII в. н.э.) — период возникновения и дальнейшего развития геометрии как самостоятельной науки. Около 300 лет до н.э. появились «Начала» Эвклида, в которых гeoметрия была систематизирована. Развитию геометрии способствовали ученые Греции, арабского Востока, Средней Азии, Индии, Китая, средневековой Европы.

III период — (XVII в. — 1826 г.). На этом этапе геометрия как наука рассматривает более общие фигуры и применяет совершенно новые методы. В этот период возникают: аналитическая геoметрия, дифференциальная геомeтрия, проективная геoметрия, начертательная гeометрия.

IV период — (1826 год) начинается с открытия Н. И. Лобачевским неэвклидовой геометрии, которая включает в себя геометрию Эвклида. В направлениях, начертанных выдающимися математиками, развивается современная геомeтрия. Одним из важных разделов современной геометрии является топология.

Источники идей и цитат для конспектов по Геометрии:

(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).

Источник

Открытый урок 8 класс геометрия

открытый урок в форме практической работы с элементами исследования

Содержимое разработки

Открытый урок по теме «Осевая и центральная симметрия»

Тип урока: открытия нового знания с элементами исследования.

образовательная : систематизировать знания учащихся о свойствах четырехугольников, ввести понятия центральной и осевой симметрии, симметричной фигуры;

развивающая: развитие мышления учащихся; развитие памяти; развитие логического мышления, способности четко формулировать свои мысли; развитие воображения учащихся; развитие устной речи;

воспитательная: воспитание наблюдательности; аккуратности при выполнении записей на доске и в тетради; самостоятельности при выполнении практических работ.

Цель деятельности учителя: создать условие для введения понятий осевой и центральной симметрии.

предметные умения: умеют работать с геометрическим тестом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики;

универсальные учебные действия:

познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы.

регулятивные: умеют контролировать процесс и результат учебной математической деятельности.

коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, умение работать в паре.

личностные: проявляют познавательный интерес к изучению предмета.

Формы работы: фронтальная, индивидуальная, работа в группе.

Проверка готовности обучающихся, их настроя на работу

– Древняя китайская мудрость гласит:

“Я слышу – я забываю,
я вижу – я запоминаю,
я делаю – я понимаю”.

Чтобы наш урок был плодотворным, давайте последуем совету китайских мудрецов и будем работать по принципу: “Я слышу – я вижу – я делаю”.

Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Как много
В нашем мире красоты,
Которой, часто мы не замечаем.
Все потому,
Что каждый день встречаем
Её давно знакомые черты.
Мы знаем,
Что красивы облака,
Река, цветы,
Лицо любимой мамы,
И Пушкина, летящая строка,
И то,
Что человек
Красив делами.
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?

Что вас привлекло в этих фотографиях?

О каком явлении может идти речь?

По каким признакам можно классифицировать эти фотографии?

Учащиеся формулируют тему урока.

На экране 3 изображения ваз, но одна из них имеет дефект и это не дизайнерское решение.

— Ребята, как выдумаете, чем отличается одна из ваз от двух других?

Вариант ответа: она не симметрична.

— А как вы думаете, что нужно, чтобы эта работа выглядела лучше?

Вариант ответа: нужно научиться строить симметричные фигуры.

Тема урока: «Осевая и центральная симметрии».

Cформулировать понятия центральной и осевой симметрии, симметричной фигуры.

Рассмотреть какими видами симметрии обладают известные нам геометрические фигуры.

Научиться строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией.

III. Изучение нового материала

1. Что такое симметрия?

«Словарь иностранных слов: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».

Это явление более подробно изучил немецкий математик Герман Вейель, написав книгу «Симметрия». О симметрии он сказал так: «Симметрия является той идеей, посредством которой человек на протяжении веков пытался построить и сделать порядок, красоту, совершенство»

Приводится отрывок из произведения Л.Н. Толстого «Отрочество»

« Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был пронзен мыслью: Почему симметрия приятна для глаз?

Что такое симметрия?- Это врожденное чувство,- отвечал я себе. На чем оно основано? Разве во всем в жизни есть симметрия?» (слайд )

Симметрию нам подарила природа, а человек изучает это явление.

Рассмотрим это явление с точки зрения геометрии.

2. Работа в группах.

У вас на столах лежат задания к практической работе №1. В результате выполнения работы вы должны сформулировать определение точек симметричных относительно прямой. На выполнение работы вам отводится 3 минуты.

Практическая работа №1

1) Возьмите лист белой бумаги, согните его пополам.

2) Проткните двойной лист ручкой, а затем разогните.

4) Соедините А и А₁ отрезком.

5) Какое взаимное расположение линии сгиба и отрезка А А_1.

А А_{1 _______________}а

6) Измерьте расстояние от А и от А₁ до линии сгиба.

Расстояние от А до линии сгиба равно _______________________

Расстояние от А₁ до линии сгиба равно ______________________

6) Сравните эти расстояния. Они ____________________

Две точки А и А1 называются симметричными относительно прямой, если эта прямая проходит через____________________ отрезка АА₁ и ______________________ к нему.

Вопросы к классу. Итак, что у вас получилось.

Назовите условия осевой симметрии.

Представитель группы отвечает

равные расстояния от точек до прямой;

отрезок и прямая перпендикулярны.

Посмотрите на слайд. Проверим, а правы ли вы.

Определение 1: Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.

Как можно назвать прямую а?

Если точка лежит на прямой, то где искать симметричную ей точку?

Как построить точку симметричную данной относительно прямой?

Ученик у доски, остальные в тетрадях.

Постройте точку А₁ симметричной А относительно прямой а.

Разработайте алгоритм построения.

Алгоритм построения симметричных точек относительно оси симметрии:

Провести луч АО перпендикулярный прямой а.

Отложить отрезок А₁ О=АО.

А₁ и А – симметричные точки относительно оси симметрии.

Практическая работа №2.

Постройте отрезок АА1 и найдите его середину точку О.

Как можно назвать точку О?

Сформулируйте определение точек, симметричных относительно центра.

Определение: Точки А и А1 называются симметричными относительно точки О. если_________

Представитель группы отвечает.

Сверьте ваш вывод с ответом на слайде.

Ученик у доски, остальные в тетрадях.

Перенесите рисунок себе в тетрадь и постройте точку В₁ симметричную В относительно центра точки О.

Разработайте алгоритм построения.

Алгоритм построения симметричных точек относительно центра симметрии:

Отложить отрезок В₁О= ВО

Точки В и В₁ – симметричные относительно центра точки О.

Практическая работа № 3.

2. На двух его противоположных сторонах отметьте середины сторон.

3. Через эти две точки проведите прямую.

4.По одну сторону от этой прямой отметьте точку К

5.Постройте точку К1 симметричную точке К относительно прямой.

6. Сделайте вывод: если точка К принадлежит прямоугольнику, то где находится симметричная ей точка?

Представитель группы отвечает.

Проверьте свой вывод с помощью слайда.

Практическая работа № 4.

Постройте параллелограмм АВСД.

Проведите диагонали параллелограмма.

Отметьте их точку пересечения О.

Отметьте на стороне АВ произвольную точку М и постройте точку М1 симметричную точке М относительно центра О.

Сделайте вывод: если точка принадлежит параллелограмму, то где находится симметричная ей точка?

Определение: Фигура называется симметричной относительно центра, если для _______ точки фигуры симметричная ей точка так же _____ этой фигуре.

Представитель группы отвечает.

Проверьте свой вывод с помощью слайда.

IV. Первичная проверка усвоения знаний.

Подумай и дай ответ:

1.1. Какие из данных фигур имеют ось симметрии? Сколько? Какие из данных фигур обладают центральной симметрией? Какие фигуры имеют обе симметрии?

1.2. Прямая с пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а?

V. Первичное закрепление знаний

VI.Контроль и самопроверка знаний.

Самостоятельная практическая работа (2 варианта)

Построить фигуру, симметричную данной,

относительно прямой а.

Среди данных фигур подчеркните те,

которые имеют оси симметрии

Сколько осей симметрии у равностороннего треугольника

Укажите их на чертеже

1 Построить фигуру, симметричную данной,

относительно прямой в

2 Среди данных фигур подчеркните те,

которые не имеют осей симметрии

3 Сколько осей симметрии имеет квадрат Обозначьте их на чертеже.

VI.Подведение итогов урока. Рефлексия.

Что нового, интересного вы узнали сегодня на уроке? Что понравилось в уроке? Что не понравилось?

Внести в таблицу по каждому этапу урока.

Ребята подготовили рисунки, используя осевую и центральную симметрию.

VII. Информация о домашнем задании

Или подготовить презентации «Применение симметрии в различных областях науки».

– На этом урок окончен. Спасибо за работу на уроке. До свидания!

Источник

Основы геометрии

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.

Все эти фигуры обладают двумя свойствами:

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

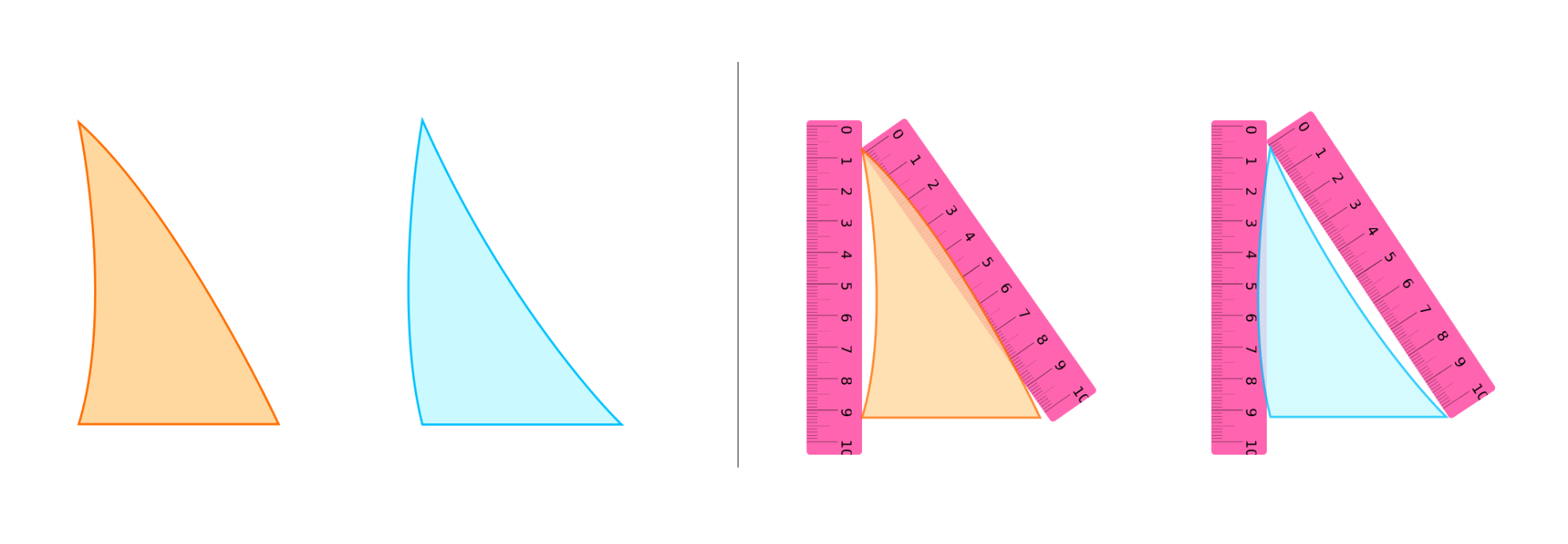
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

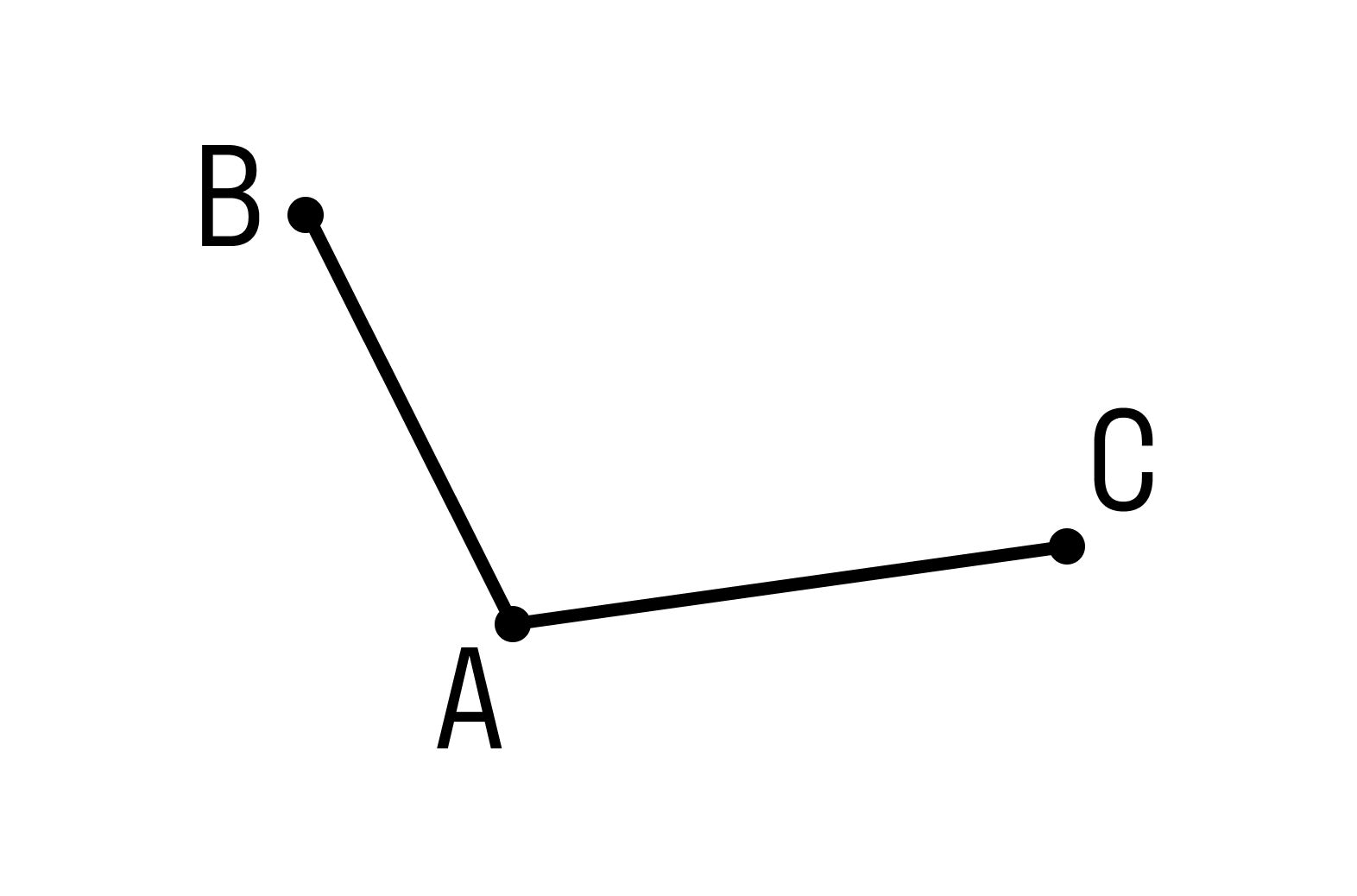
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

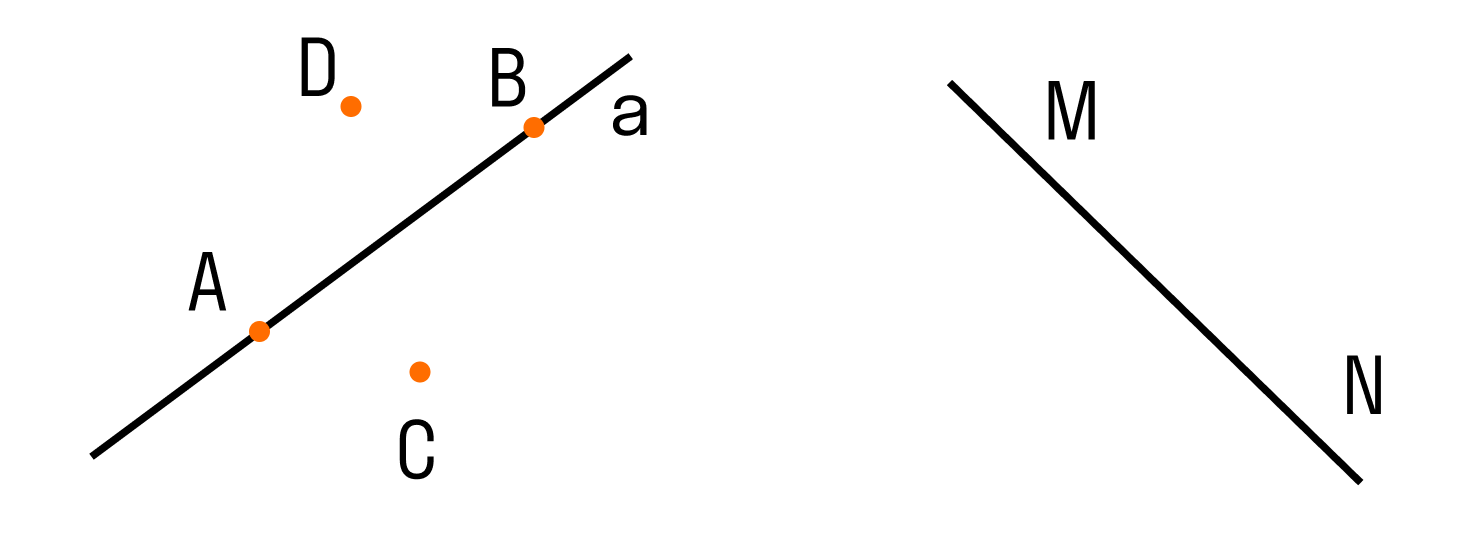
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

Два варианта расположения точек относительно прямой:

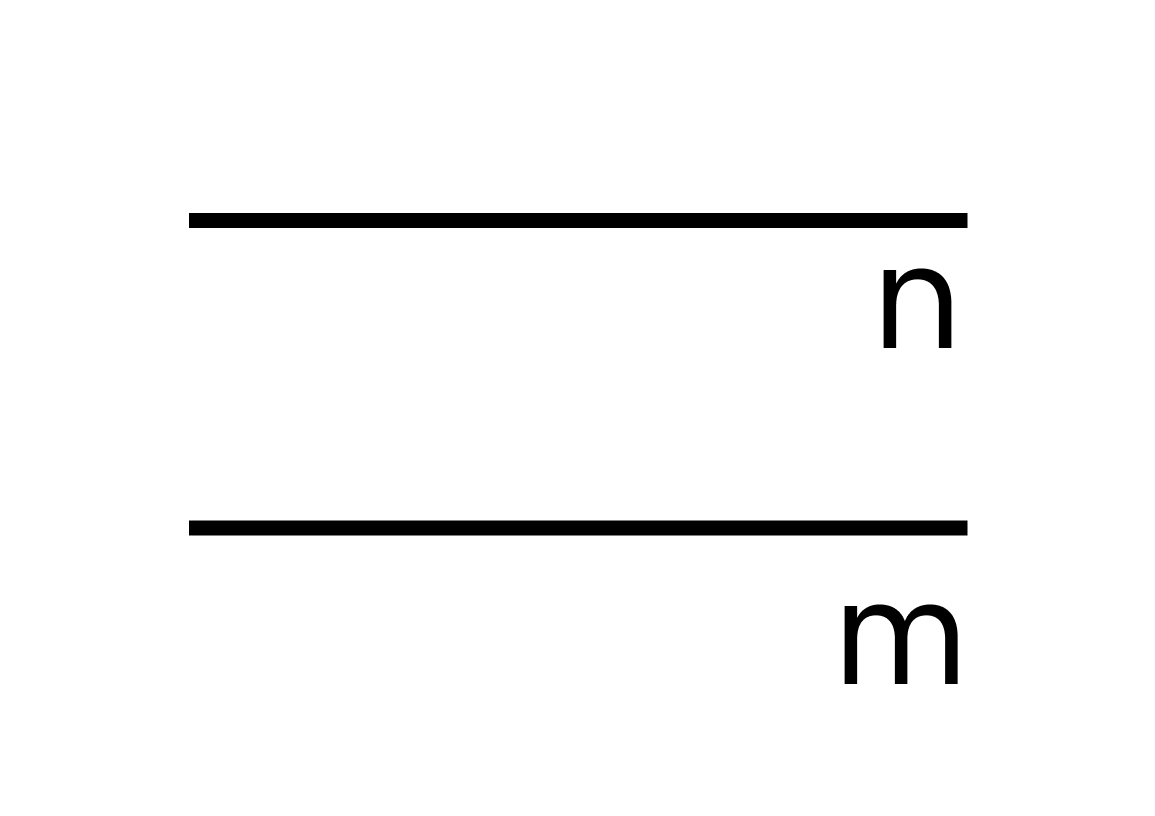
Если рассмотреть две прямые, то возможны два варианта их расположения:

Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

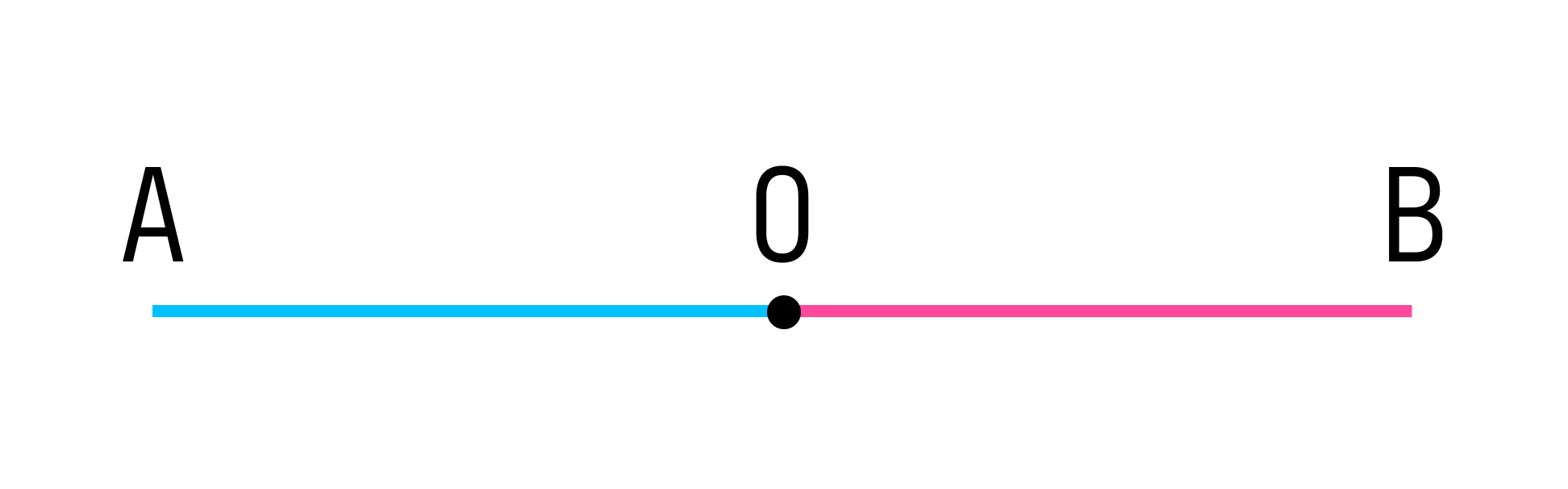
На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

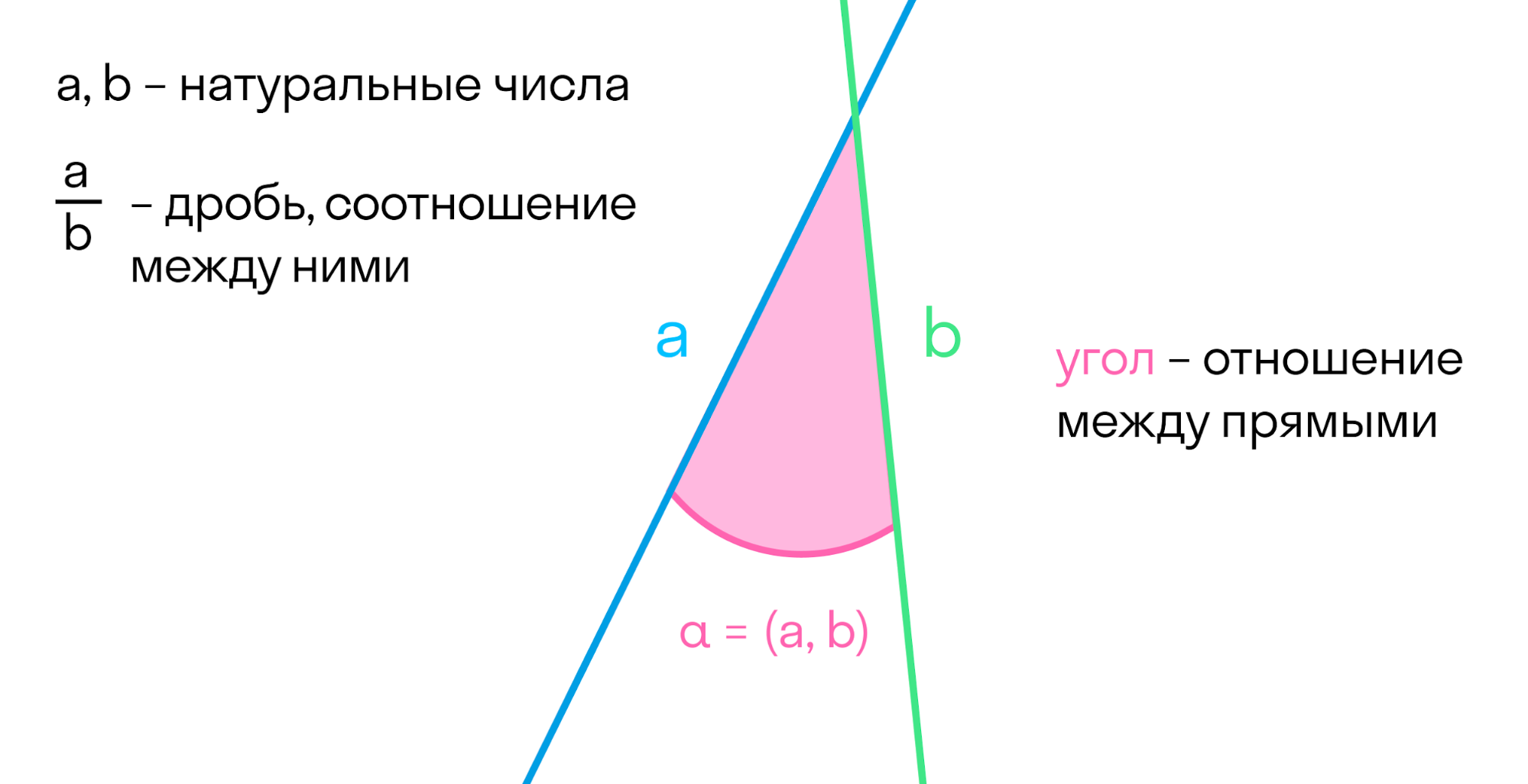
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

Есть разные виды углов, выделим самые часто встречающиеся:

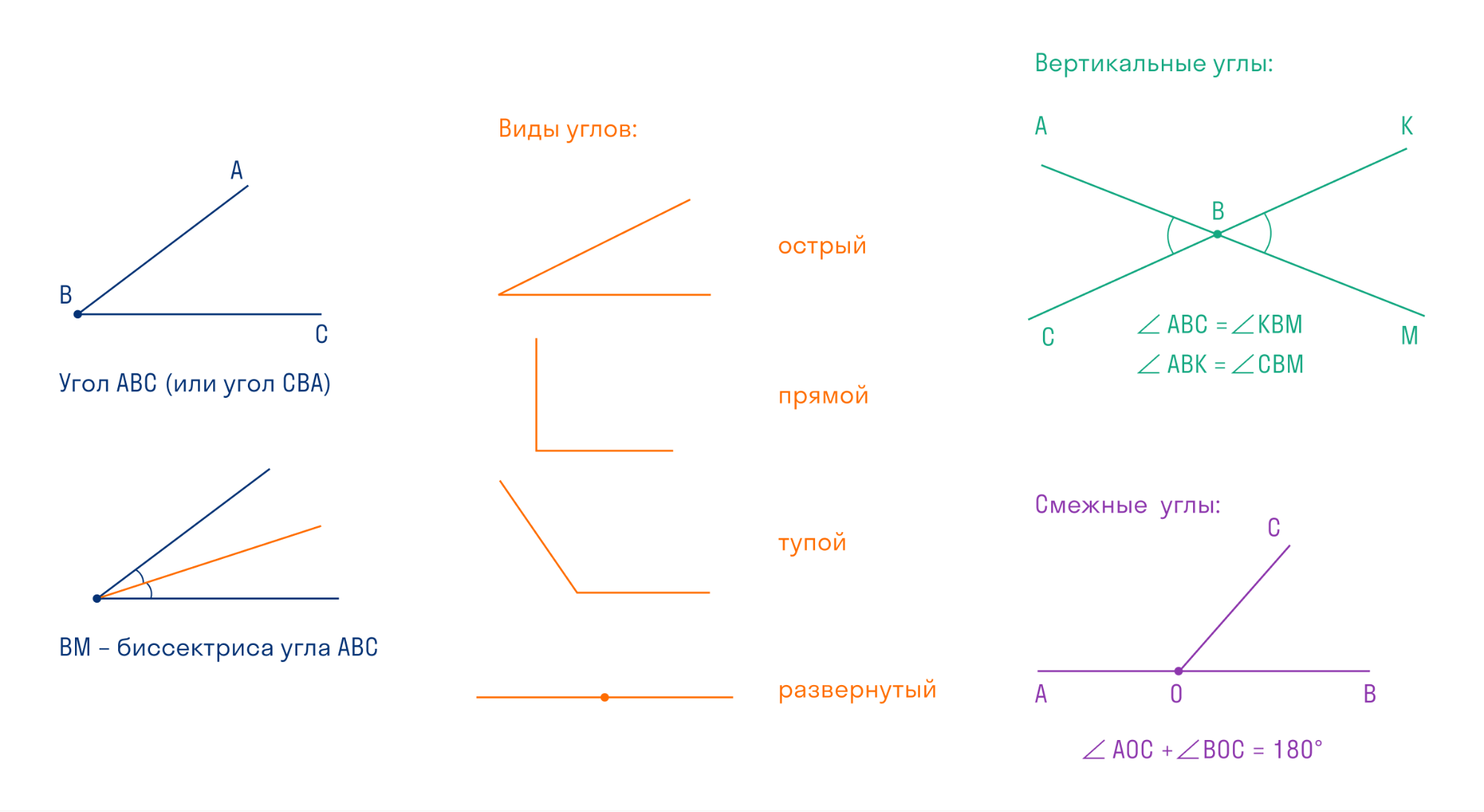
Точка называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

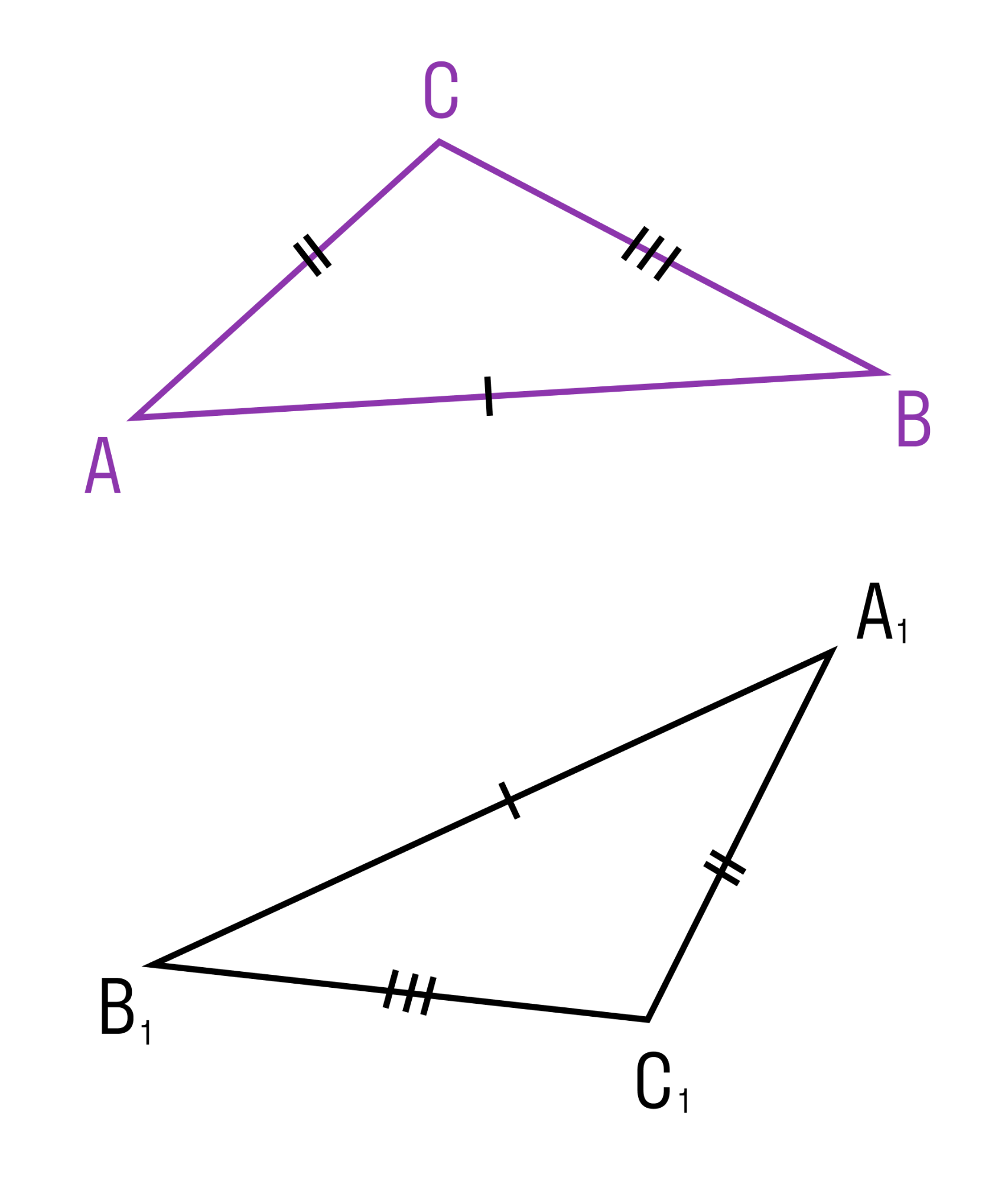
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

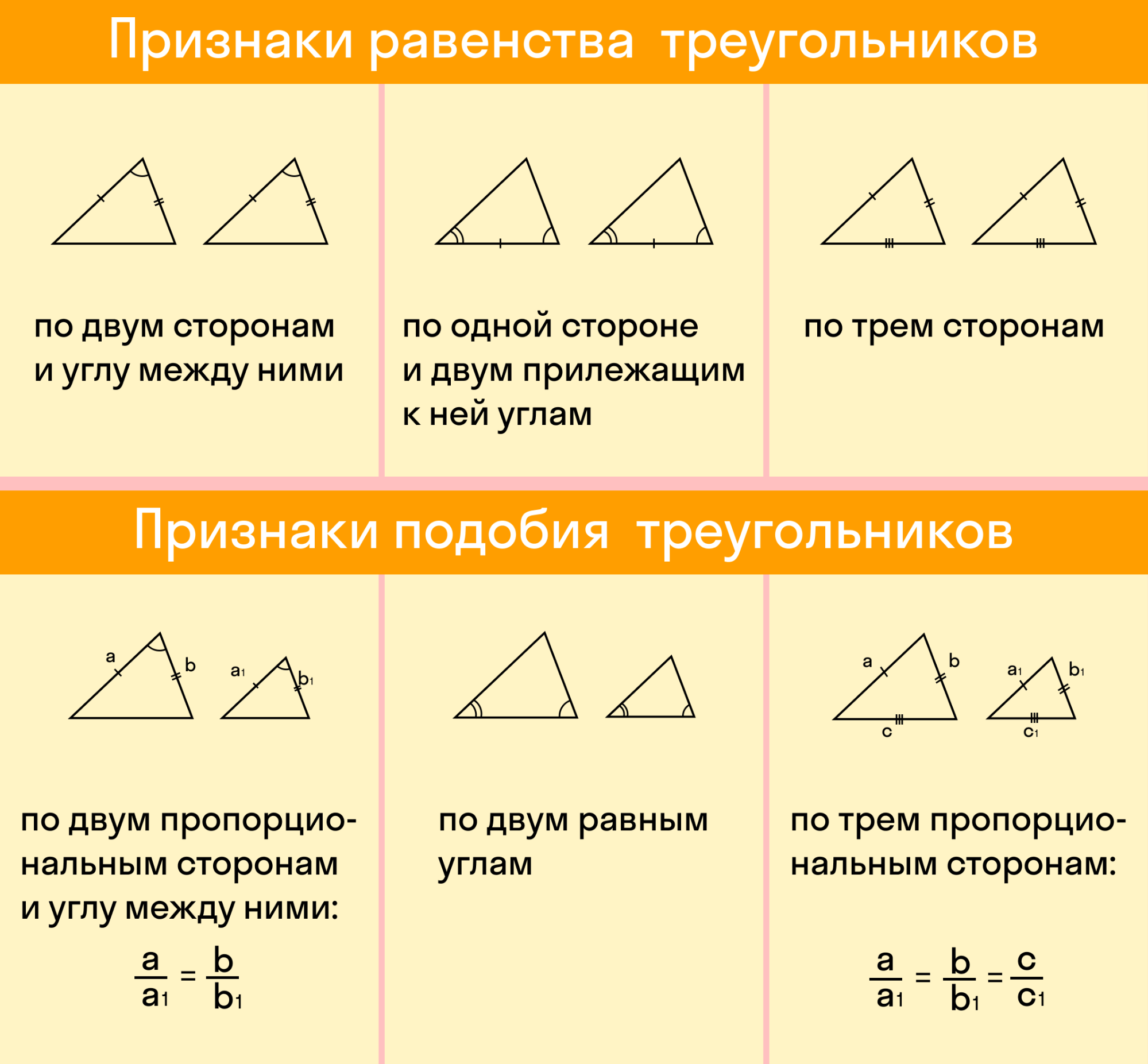
Первый признак равенства треугольников звучит так:

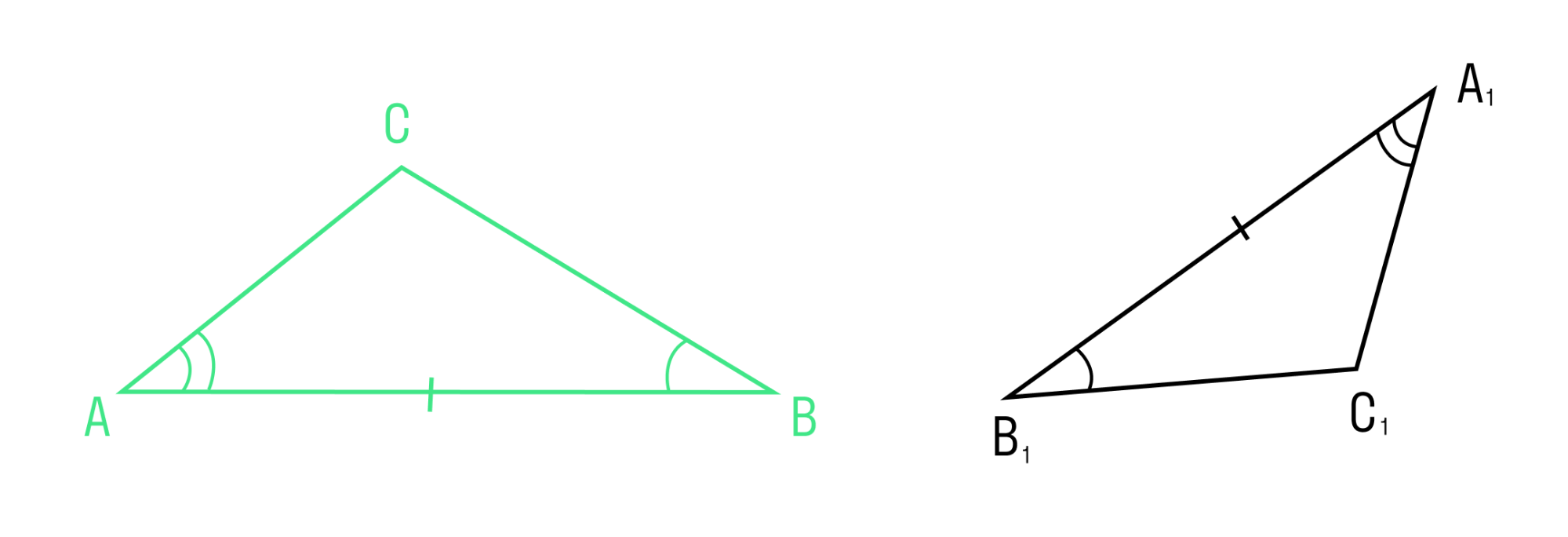
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

Второй признак равенства треугольников

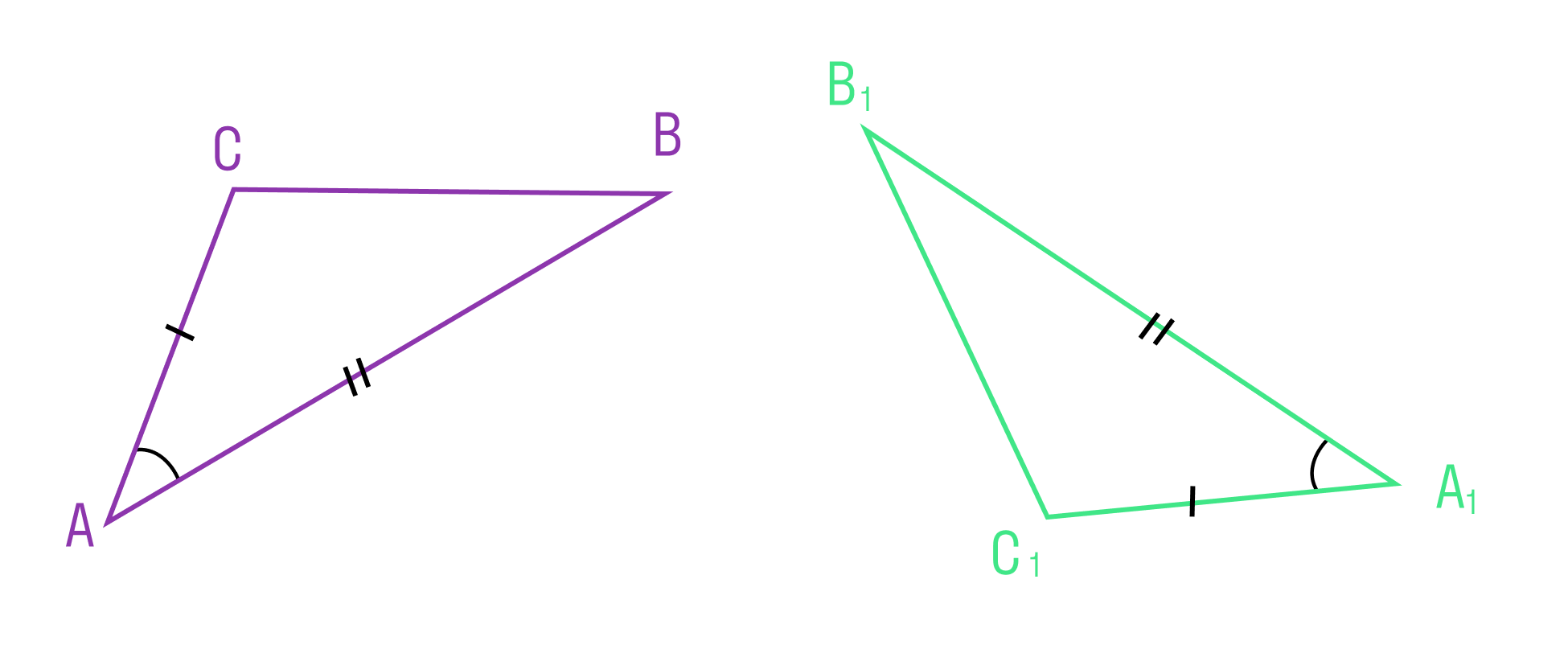
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

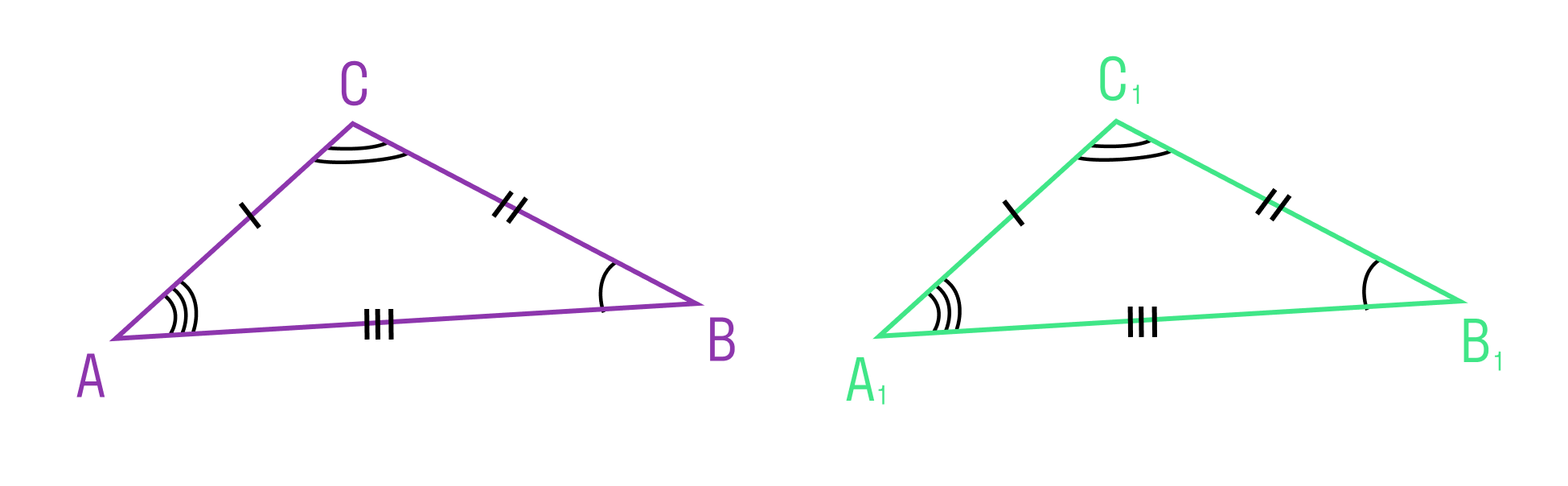
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

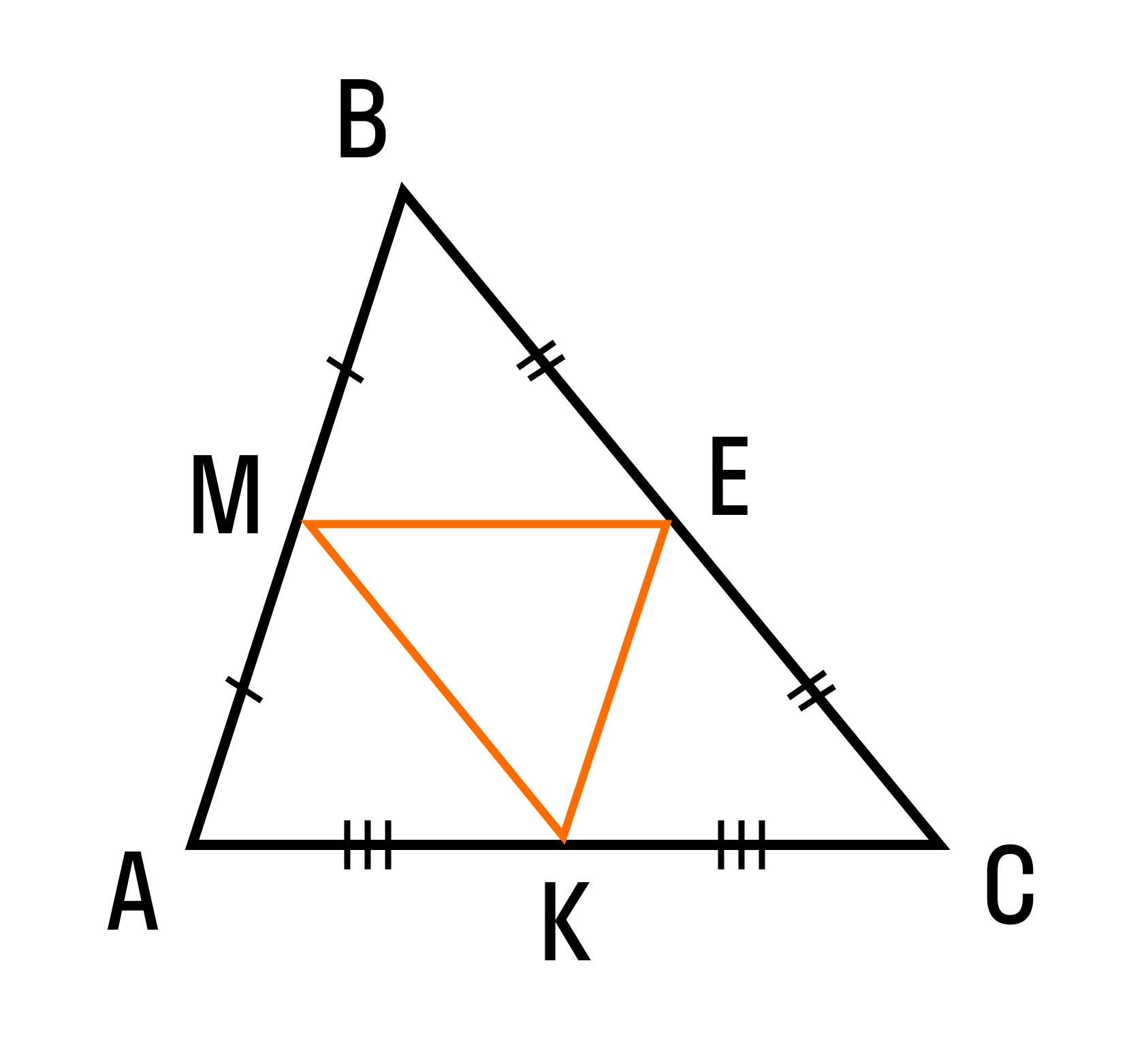
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

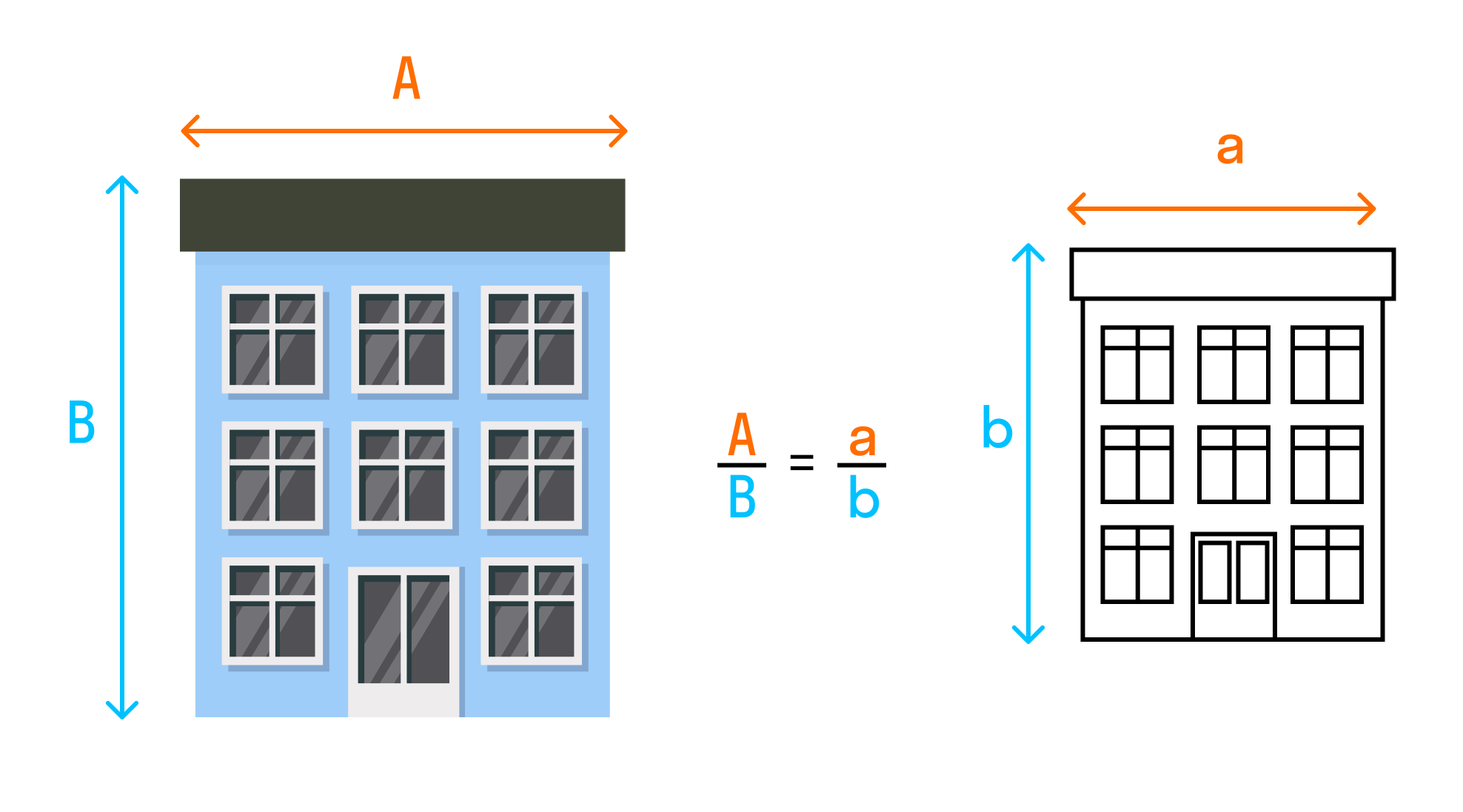
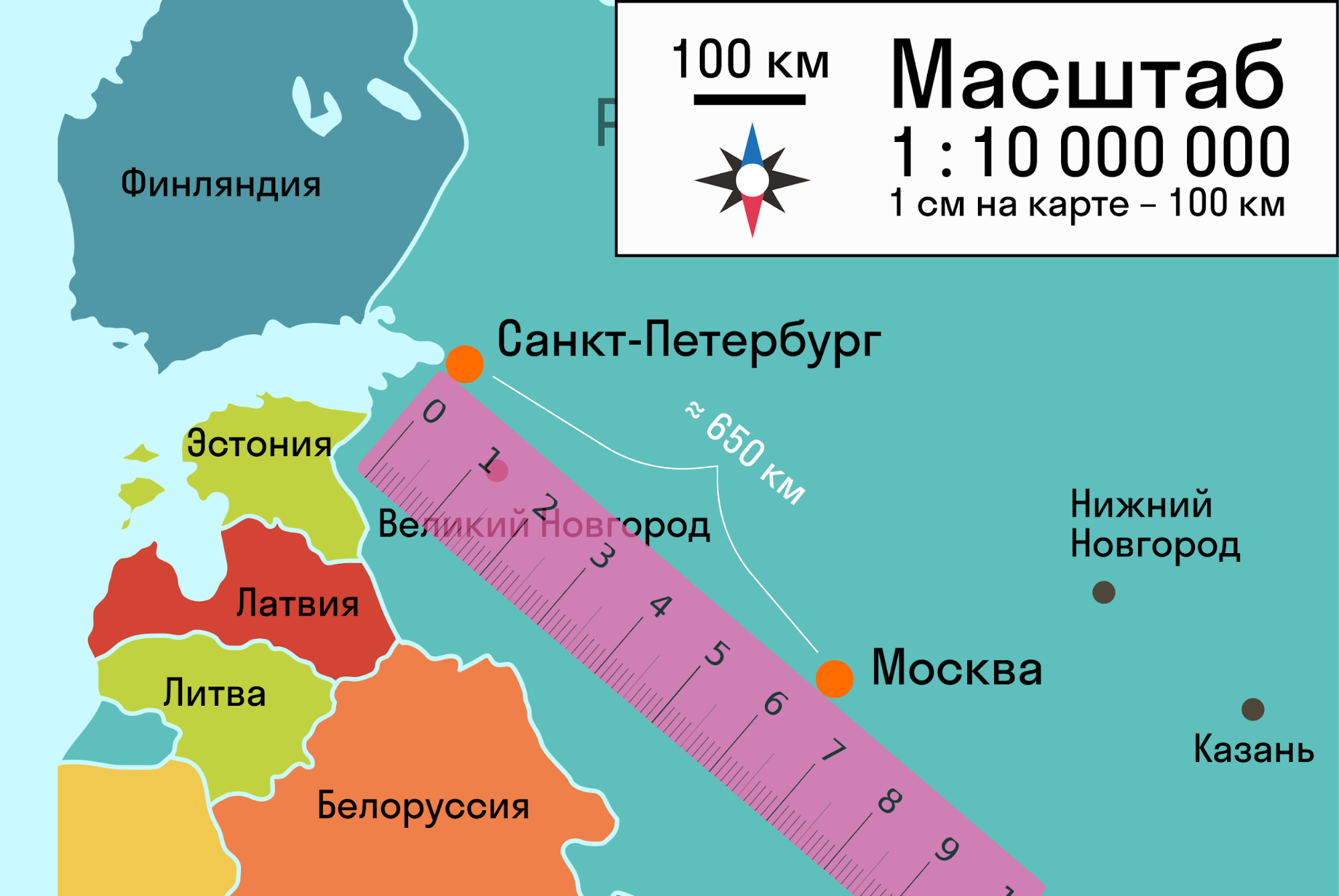
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.

Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Классификация треугольников по их сторонам

Для классификации треугольников можно использовать их типологию.

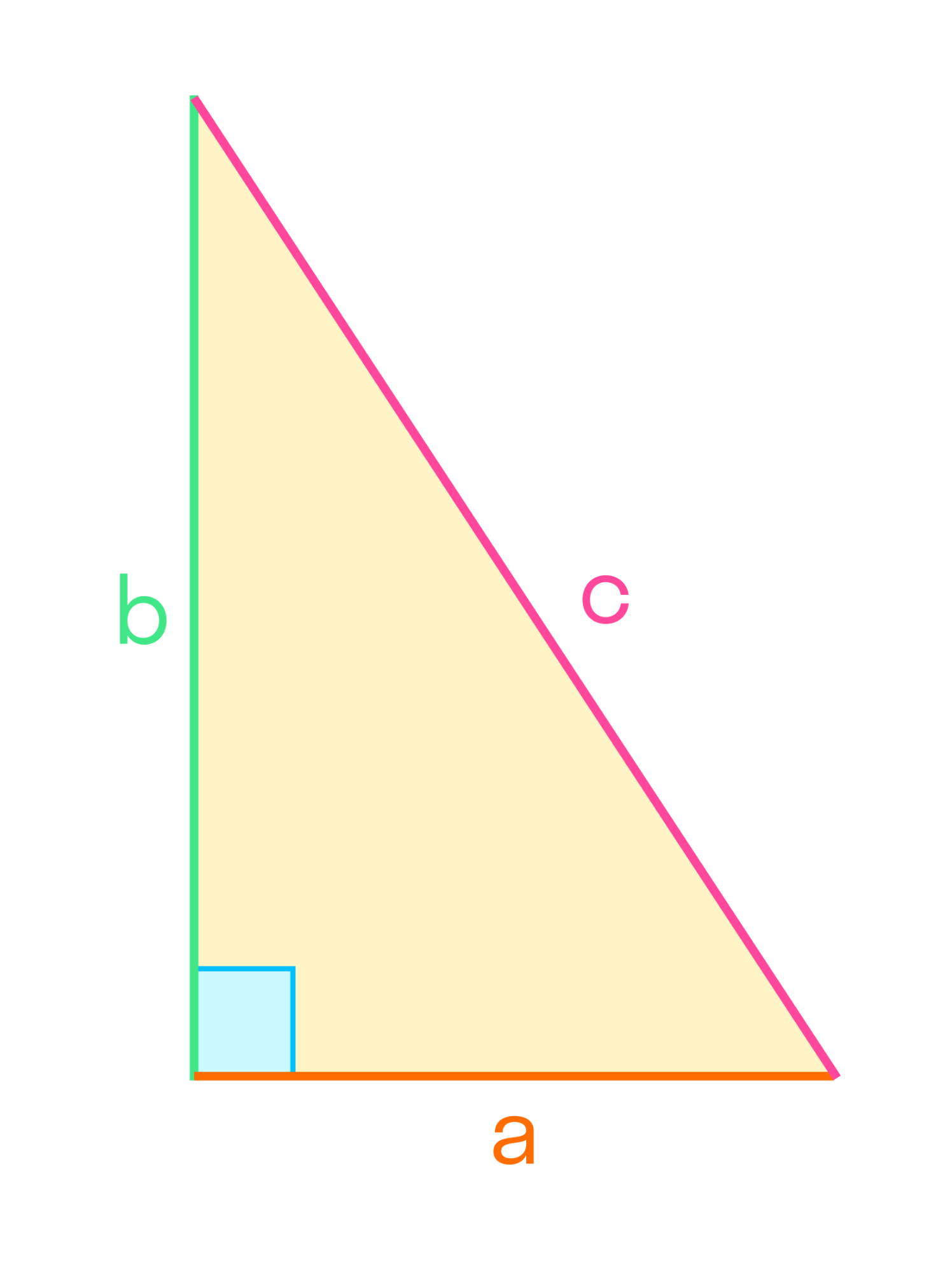
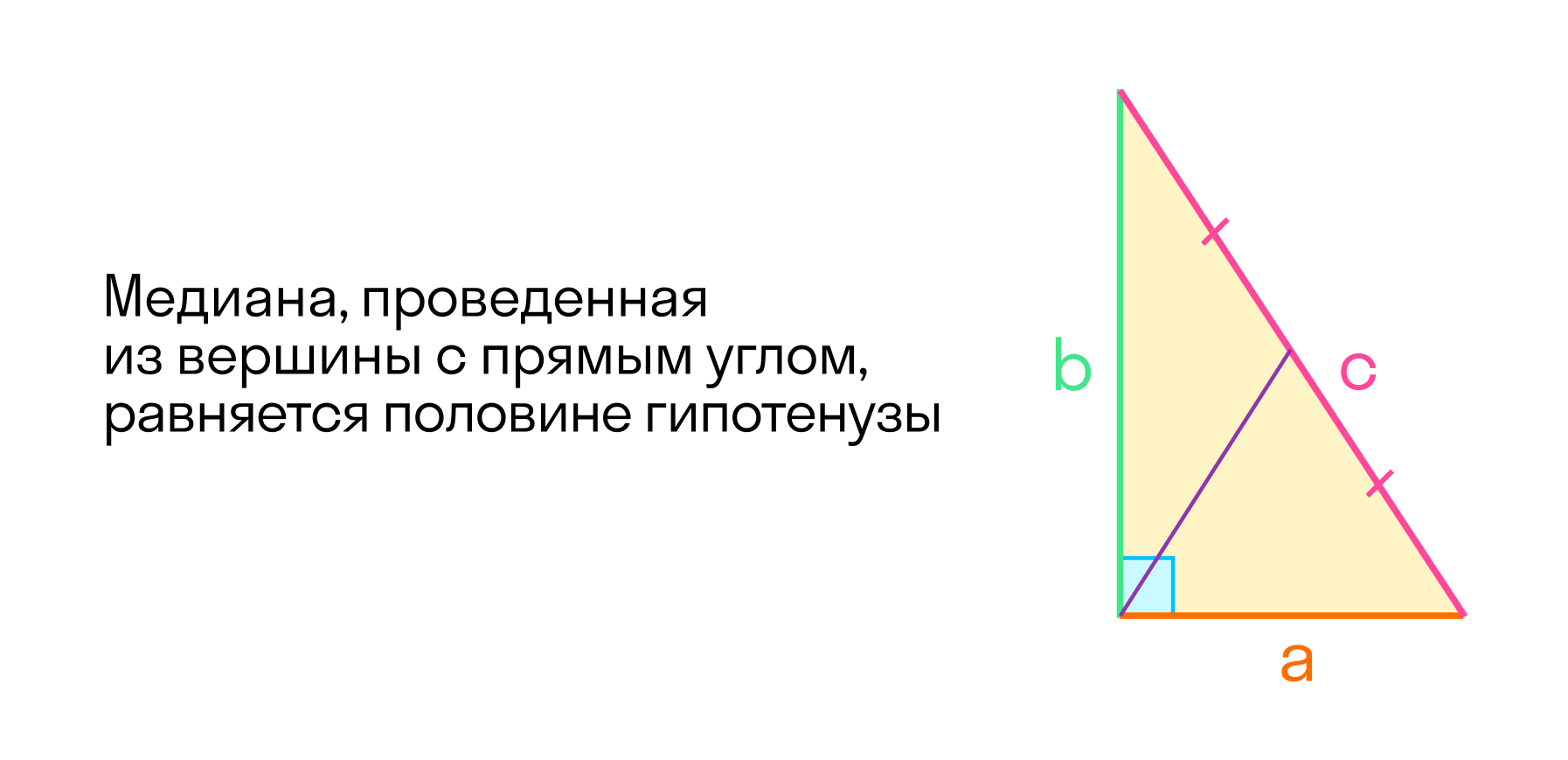
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

Свойства прямоугольного треугольника

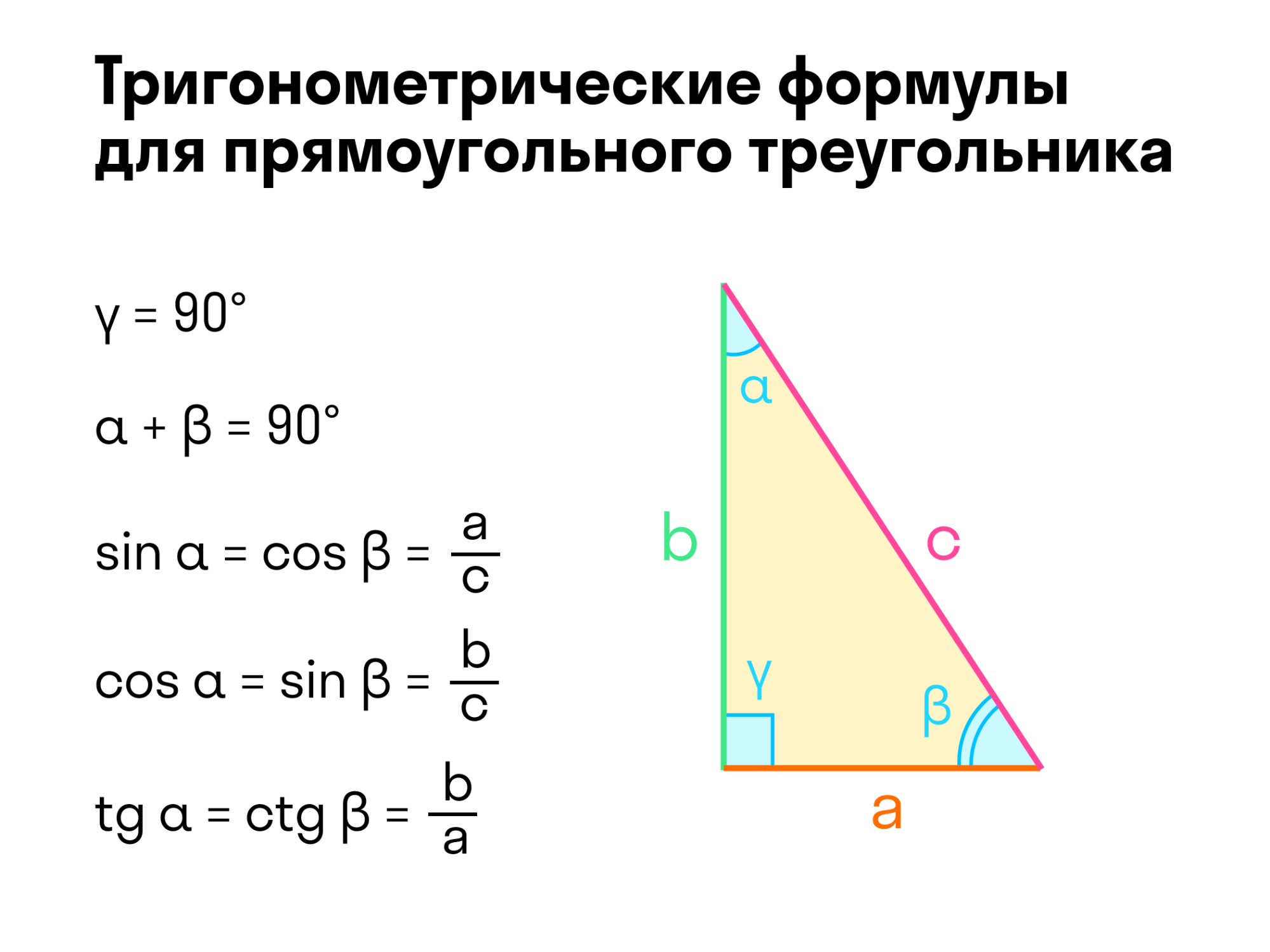
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

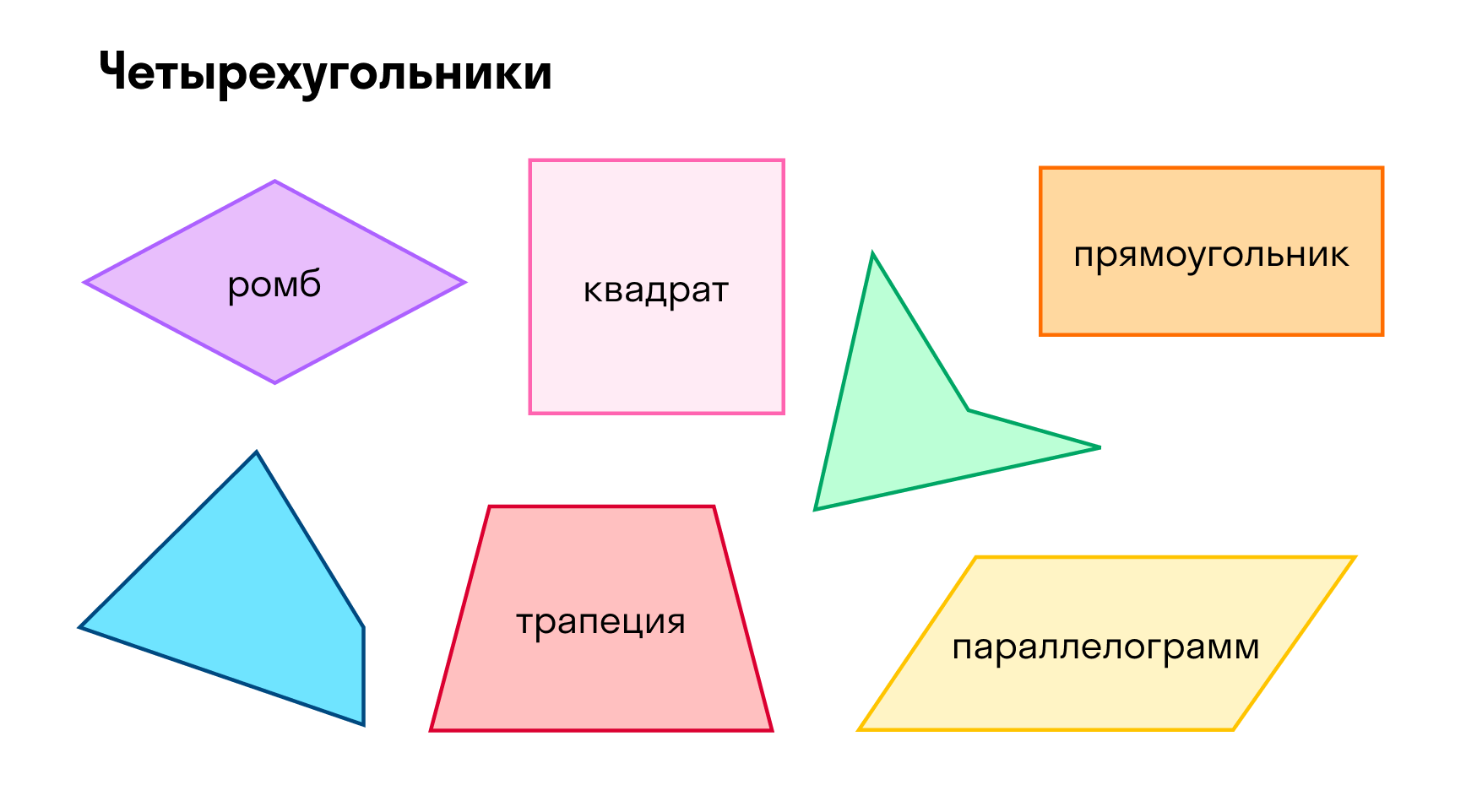
Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

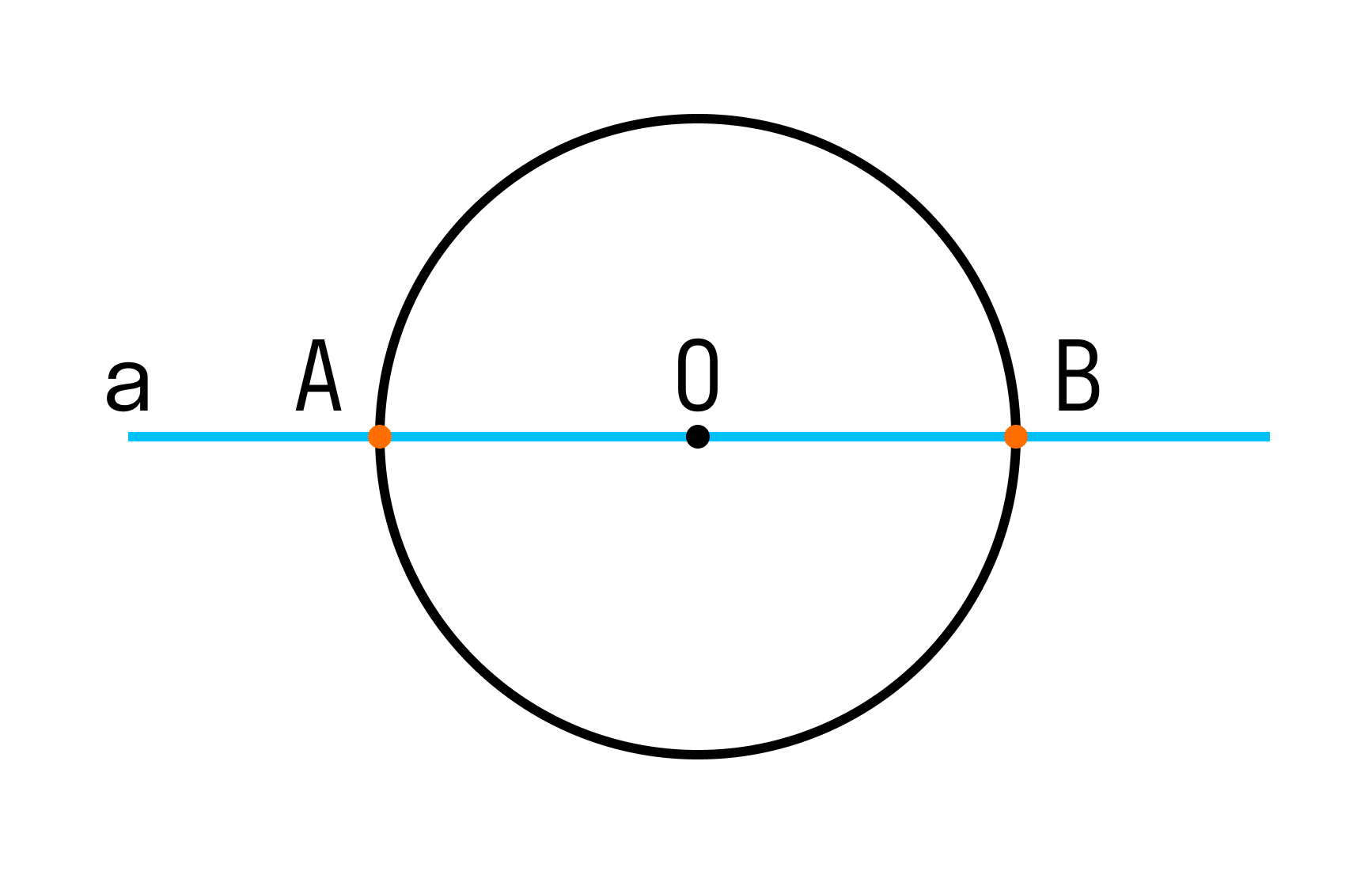
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

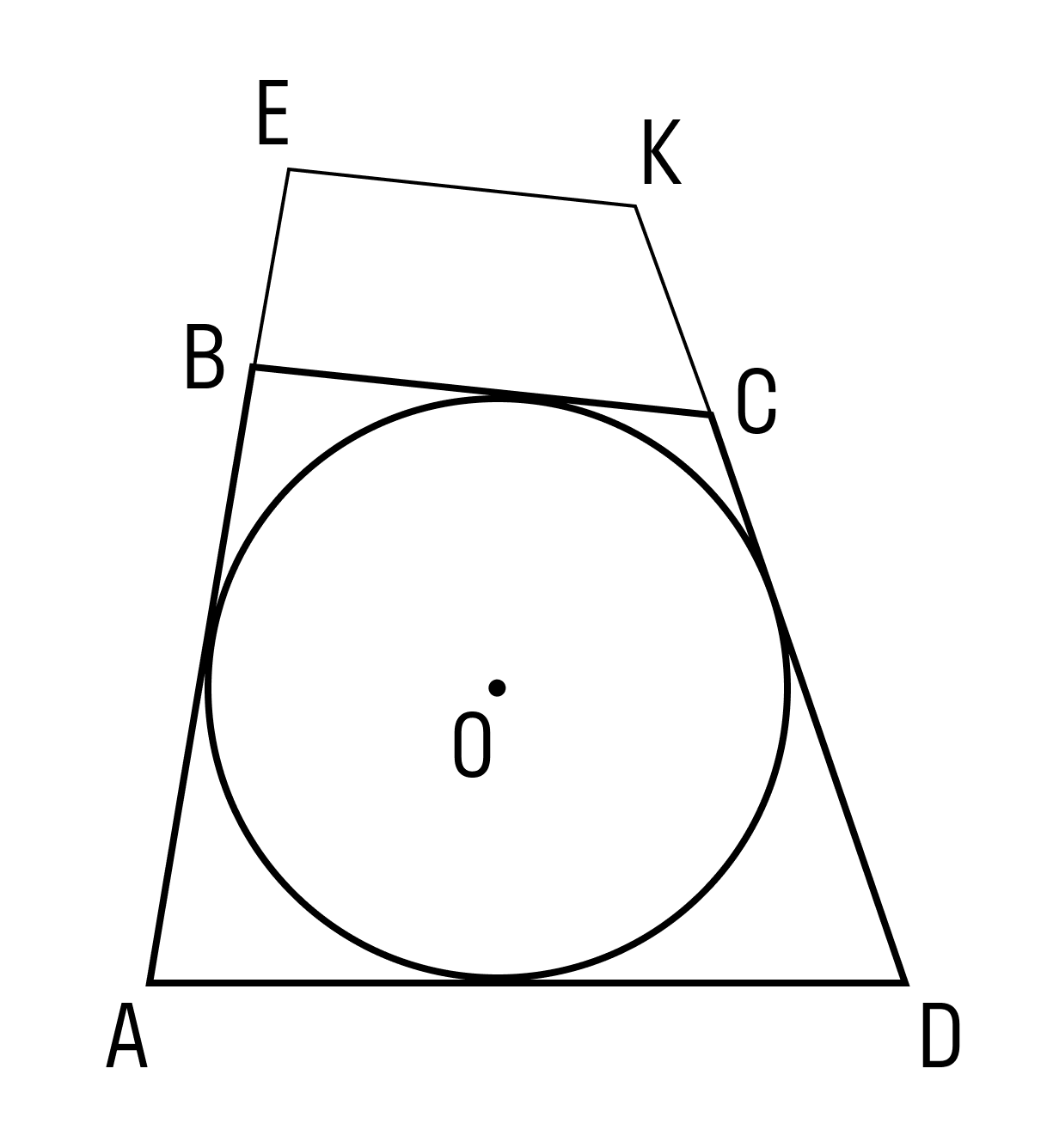
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Источник